Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 27

3.27. Se o cilindro E pesa 150   N e θ = 15 ° , determine o peso do cilindro F.

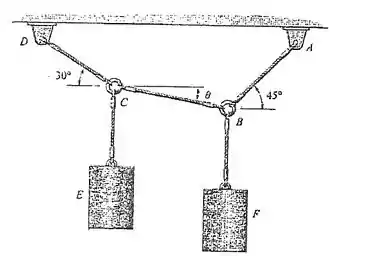
Passo 1

Fala! Queremos achar o peso de F .

Para esse exercício devemos analisar o diagrama de corpo livre, da argola em C e em B :

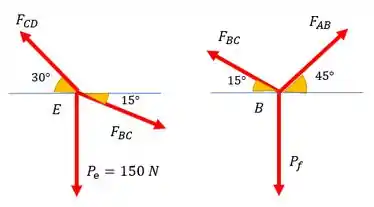
Vamos descobrir P f aplicando as equações de equilíbrio nesses pontos. Percebe que no ponto B , onde temos P f , não sabemos F B C . Por isso, vamos analisar o ponto E   para encontrar essa forcinha, e depois ir para B e encontrar o peso.

Bora!

Passo 2

Vamos começar em C . O somatório de forças nas direções x e y precisam ser zero, então fazemos:

∑ F x = 0

F B C ⋅ cos ⁡ 15 ° - F C D ⋅ cos ⁡ 30 ° = 0

Repara que a gente decompôs nossas forças no eixo horizontal.

Então

F B C ⋅ cos ⁡ 15 ° = F C D ⋅ cos ⁡ 30 °

F C D = F B C cos ⁡ 15 ° cos ⁡ 30 °

Agora vamos fazer o mesmo para y :

∑ F y = 0

Decompondo nossas forças no eixo vertical:

- F B C ⋅ sin ⁡ 15 ° + F C D ⋅ sin ⁡ 30 ° - 15 0 = 0

Passo 3

Agora vamos resolver essas equações substituindo a primeira na segunda

- F B C ⋅ sin ⁡ 15 ° + F C D ⋅ sin ⁡ 30 ° - 150 = 0

- F B C ⋅ sin ⁡ 15 ° + F B C cos ⁡ 15 ° cos ⁡ 30 ° ⋅ sin ⁡ 30 ° - 150 = 0

Calculando esses valores de seno e cosseno e isolando F B C :

F B C = 501,91   N

Prontinho, achamos F B C .

A gente não precisa de F C D . Não vamos nem calcular.

Passo 4

Partimos para achar P f nas equações de equilíbrio no ponto B

Para o eixo x :

∑ F x = 0

F B A   cos ⁡ 45 ° - F B C cos ⁡ 15 ° = 0

Então

F B A = F B C ⋅ cos ⁡ 15 ° cos ⁡ 45 ° = 501,91 ⋅ cos ⁡ 15 ° cos ⁡ 45 ° = 685,62   N

Agora vamos fazer o mesmo para o eixo y :

∑ F y - 0

F B A ⋅ sin ⁡ 45 ° + F B C ⋅ sin ⁡ 15 ° - P f = 0

685,62 ⋅ sin ⁡ 45 ° + F B C ⋅ sin ⁡ 15 ° - P f = 0

Então

P f = 685,62 ⋅ sin ⁡ 45 ° + 501,91   ⋅ sin ⁡ 15 ° = 614 , 7 1   N

Resposta

P f = 614,71   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três cabos são unidos no anel de junção C . Determine as tensões nos cabos A C e B C causadas pelo peso do cilindro de 30k g .
A barra delgada uniforme de ângulo reto A O B tem massa m . Se o atrito no pivô O for desprezado, determine a magnitude da força normal em A e a magnitude da reação do pino em O .
Um lenhador deseja fazer com que o tronco da árvore caia colina acima, embora o tronco esteja inclinado para baixo. Com o auxílio do guincho W, que tensão T no cabo será necessária? O tronco de 1200l
A alavanca “deadman” controla as brocas de um removedor de neve. Se uma força F=30N é necessária para começar a girar a alavanca em torno do pivô ideal em O , determine a tensão correspondente T no ca
Encontre o ângulo de inclinação θ com a horizontal de forma que a força de contato em B seja a metade daquela em A para o cilindro liso.