Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 225
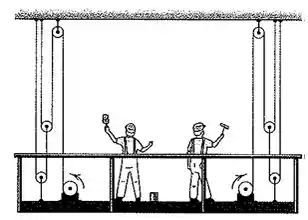
2/225) Os guinchos motorizados sobre o andaime industrial permitem que este seja elevado ou abaixado . Para a rotação no sentido indicado , o andaime está sendo elevado . Se cada tambor tem um diâmetro de e gira na taxa de , determine a velocidade de subida do andaime .
Passo 1
Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento dos 2 cabos que aparecem na imagem . E para isso , definimos que :
é a distância do centro da polia mais elevada até o centro da polia menos elevada .
é a distância do centros das polias da 2° e 3° fileira horizontal de polias .
Com essas propriedade definidas , temos que :
O comprimento é dado por :
O comprimento é :
Passo 2
Como de costume , derivaremos as equações de comprimento para obtermos relações com as velocidades :
Derivando :
Usando a relação , achamos que :
Derivando :
Como , temos que :
Portanto ,
Resposta
De boa galera? Bora fazer mais exercícios então!