Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 222

2/122) Determine uma expressão para a velocidade v A do carrinho A descendo a inclinação em termos da velocidade de subida v B do cilindro B .

Passo 1

Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento do cabo que aparece na imagem . E para isso , definimos que :

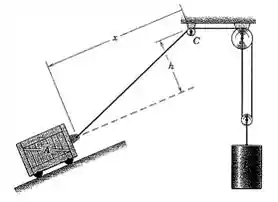
x   é a distância do centro da polia menor até o carrinho .

y   é a distância do centro da polia maior até o centro da polia que sustenta o bloco B .

h é a distância vertical expressa na imagem do enunciado .

Com essas propriedades definidas , temos que o comprimento total do cabo é dado por :

L = x 2 + h 2 + 2 y + c o n s t a n t e

Passo 2

Agora , como já estamos acostumados , derivaremos a equação do comprimento do cabo para obtermos uma relação com sua velocidade :

L ' = 0 = 1 2 2 x x ' x 2 + h 2 + 2 y '

Como v A ' = x ' e v B = - y ' , achamos que :

v A = + 2 x 2 + h 2 x v B

Resposta

v A = + 2 x 2 + h 2 x v B

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a carga B tem uma velocidade para baixo v B , determine a componente ascendente v A y da velocidade de A em termos de b , do comprimento da haste l e do ângulo θ . Suponha que o cabo que suporta A
O cilindro A tem uma velocidade constante para baixo de 1m / s . Calcule a velocidade do cilindro B para (a) θ = 45 ° , (b) θ = 30 ° , (c) θ = 15 ° . A mola está sob tração durante toda a faixa de int
2/224) Determine a elevação vertical h dacarga W durante 10 segundos se o tambor de elevação recolhe o cabo na taxa constante de 180 m m / s .
2/120) Para um dado valor de y , determine a velocidade ascendente de A em termos da velocidade descendente de B . Despreze os diâmetros das polias .
Sob ação da força P , a aceleração constante do bloco B é de 3m / s ² ² para a direita. No instante em que a velocidade de B é de 2m / s para a direita, determine a velocidade de B em relação a A , a