Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 213
Se o bloco tem uma velocidade de para a direita, determine a velocidade do cilindro .
Passo 1
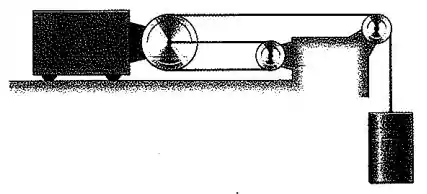
Galera, considere como a distância entre as duas polias mais próximas do bloco , que pode se mover na horizontal. E considere como a distância do bloco à outra polia. Temos que o comprimento total da corda é:
Portanto, se derivarmos em relação ao tempo, obteremos:
pois o comprimento é constante. Obtemos então a relação entre as velocidades dos dois blocos:
Ou seja,
Logo, o bloco tem a velocidade de para baixo.
Resposta
para baixo
Exercícios de Livros Relacionados
Determine a equação de restrição que relaciona as acelerações dos corpos A e B . Assuma que a superfície superior de A permanece na horizontal.
Se a velocidade x ˙ do bloco A subindo o plano inclinado está aumentando na taxa de 0,044m / s cada segundo, determine a aceleração de B .
2/122) Determine uma expressão para a velocidade v A do carrinho A descendo a inclinação em termos da velocidade de subida v B do cilindro B .
2/121) Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de A e a velocidade de B para um determinado valor de y .