Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 214
Se a velocidade do bloco subindo o plano inclinado está aumentando na taxa de cada segundo, determine a aceleração de .
Passo 1
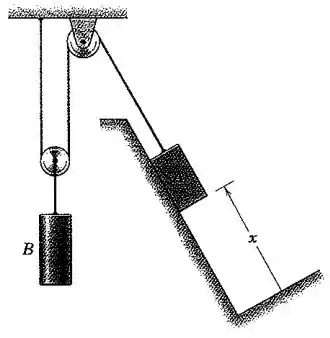
Galera, considere como a distância entre o bloco e a polia fixa no teto e como a distância da polia móvel (que se move junto ao bloco ) à polia fixa no teto. Temos que o comprimento total da corda é:
Portanto, se derivarmos em relação ao tempo, obteremos:
Derivando mais uma vez:
Passo 2
Repare que, à medida que a distância aumenta, a distância entre o bloco e a parede diminui, ou seja:
Então, obtemos a seguinte relação entre as acelerações dos dois blocos:
Conforme o enunciado, temos , ou seja:
Resposta
Exercícios de Livros Relacionados
2/225) Os guinchos motorizados sobre o andaime industrial permitem que este seja elevado ou abaixado . Para a rotação no sentido indicado , o andaime está sendo elevado . Se cada tambor tem um diâmetr
2/1228) Os anéis A e B deslizam ao longo das hastes fizas em ângulo reto e estão conectados por um fio de comprimento L . Determine a aceleração a x do anel B em função de y se o anel A possui uma vel
2/223)Sob aação da força P , aaceleração constante do bloco B é de 2 m / s 2 para cima do plano inclinado . Para o instante em que a velocidade de B é de 1,2m / s subindo o plano inclinado , determine
2/227) A fim de acelerar a elevação dos fardos representados no exemplo 2/16 , o arranjo das polias é alterado como mostrado aqui . Se o trator A tem uma velocidade para a frente v A , determine uma e
2/226) O andaime do Prob.2/225 é modificado aqui pela colocação dos guinhos motorizados no chão em vezde no andaime . As outras condições permanecem as mesmas . Calcule a velocidade de subida v do and