Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 221
2/121) Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de A e a velocidade de B para um determinado valor de .
Passo 1
Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento do cabo que aparece na imagem . E para isso , definimos que :
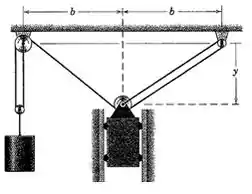
é a distância do centro da polia mais à esquerda presano teto até o centro da polia que sustenta o bloco mais à esquerda .
é a distância do centro da polia mais à direita até o centro da polia central .
é a distância que separa as duas polias que estão presas no teto .
Tendo isso definido , o comprimento total do cabo é dado por :
Passo 2
Como de costume , derivaremos a equação do comprimento do cabo para obtermos uma relação entre as velocidades :
Onde ,
Sendo assim , nós temos que :
Resposta
De boa galera? Bora fazer mais exercícios então!