Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 55

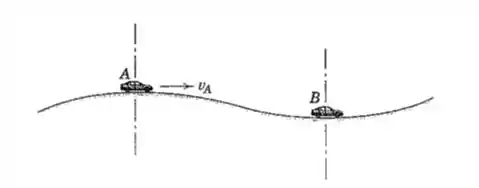
3/55) O carro passa sobre o topo de uma curva num plano vertical em A com uma velocidade de 60   k m / h e então passa pelo fundo de uma depressão em B . Os raios de curvatura da estrada em A e B são ambos 100   m . Encontre a velocidade do carro em B se a força normal entre a estrada e os pneus em B é o dobro daquela em A . O centro de massa do carro está a 1 metro da estrada .

Passo 1

Bom pessoal , novamente teremos que aplicar o princípio do somatório das forças concorrentes para resolvermos a questão . Nesse caso , iremos dividir a análise em cada um dos pontos da trajetória . Temos que :

∑ F n = m a n  

Para o ponto A :

  m g - N A = m v A 2 ρ A

Para o ponto B :

B   : N B - m g = m v B 2 ρ B

Passo 2

Agora usaremos a condição que nos foi imposta de que a força normal entre a estrada e os pneus em B é o dobro daquela em A .

Para N B = 2 N A :

m v B 2 ρ B + g = 2 m g - v A 2 ρ A

Isolando v B 2 na equação , obtemos que :

v B 2 =   ρ B g - 2 v A 2 ρ A ρ B = 99 9,81 - 2 60.1000 3600 2 99 101 = 427 m 2 / s 2  

Basta tirarmos a raiz quandrada para acharmos a velocidade do carro em B :

v B = 20,7   m / s

Resposta

v B = 20,7   m / s

Suave galera? Então bora resolver mais questões como essa!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o coeficiente mínimo de atrito estático entre os pneus e a superfície da estrada de maneira que o carro de 1,5 Mg não deslize quando ele se move a 80 km/h na estrada em curva. Despreze a dim
Determine a velocidade máxima na qual o carro com massa m pode passar sobre o ponto mais alto A da estrada em curva vertical e ainda manter o contato com a estrada. Se o carro mantém esta velocidade,
Uma bola tem massa m e está ligada à corda de comprimento l . A corda está amarrada no topo a uma argola móvel e é dada uma velocidade v 0 à bola. Demonstre que o ângulo θ que a corda faz com a vertic
Um avião de 5 Mg está voando com uma velocidade constante de 350 km/h ao longo da trajetória circular horizontal de raio r = 3000m . Determine a força de sustentação L atuando sobre o avião e o ângulo
No instante mostrado, o carro de 1500 kg está se movendo com velocidade de 25 m/s, a qual está crescendo a uma taxa de 2m / s 2 . Determine a intensidade da força de atrito resultante que a estrada ex