2.26. A tora deve ser rebocada por dois tratores A e B. Determine as intensidades das duas forças de reboque e , levando-se em conta que a força resultante tenha uma intensidade e seja orientada ao longo do eixo x. Considere .

Passo 1
Fala! Queremos as forças dos tratores para rebocar a tora, causando uma resultante de .
Se essa é a resultante, podemos escrever vetorialmente que
Vamos analisar as forças , e como vetores, e aí poderemos usar a lei dos paralelogramos para achar nossas incógnitas. Vamos fazer um esquema da nossa situação
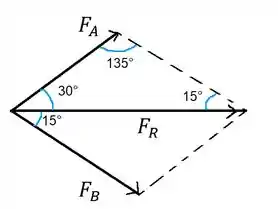
Temos na direção de . Percebe que esse ângulo de aparece porque esse segmento tracejado é paralelo a linha da força de . E esse aparece, porque a soma interna de ângulos de um triângulo é .
Daqui podemos extrair o seguinte triângulo
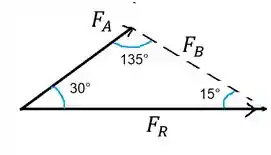
Passo 2
Vamos calcular as forças usando a lei dos senos
Passo 3
Agora vamos calcular