Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 113

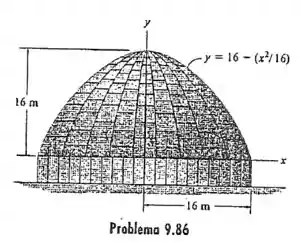
9.86 Determine a área da superfície da cobertura da estrutura se ela é formada girando-se a parábola em torno do eixo y .

Passo 1

A fórmula para determinar a área é:

A = θ r - L

Onde θ é o ângulo de revolução em radianos, nesse caso 2 π

Para descobrirmos o tamanho L da curva, devemos resolver a integral:

L = ∫ L d L

Um pedacinho “ d L ” dessa curva pode ser calculada usando pitagoras:

d L 2 = d x 2 + d y 2

d L = d x 2 + d y 2

d L = d x 2 1 + d y d x 2

Podemos tirar d x da raiz quadrada

d L = 1 + d y d x 2 d x

d y d x vai ser a derivada da função:

d y d x = - x 8

Substituindo:

d L = 1 + - x 8 2 d x

d L = 1 + x 2 64 d x

Agora é só calcular a integral para descobrir o tamanho da curva, sabendo que devemos integrar de 0 até 16:

L = ∫ 0 16 1 + x 2 64 d x

Precisamos usar uma substituição trigonométrica para resolver a integral, vamos falar que:

x = 8 tg ⁡ u

d x = 8 sec 2 ⁡ u   d u

Os limites de integração vão ser:

x = 0

8 tg ⁡ u = 0

u = 0

e

x = 16

8 tg ⁡ u = 16

tg ⁡ u = 2

u = arctg ⁡ 2

E a integral vai ficar:

L = ∫ 0 arctg ⁡ 2 1 + 8 tg ⁡ u 2 64 8 sec 2 ⁡ u d u

L = 8 ∫ 0 arctg ⁡ 2 1 + tg 2 ⁡ u sec 2 ⁡ u d u

Podemos usar a relação trigonométrica:

sec 2 ⁡ u = 1 + tg 2 ⁡ u

Isolando a secante, vamos obter:

sec ⁡ u = 1 + tg 2 ⁡ u

Agora podemos reescrever a integral, como sendo:

L = 8 ∫ 0 arctg ⁡ 2 sec ⁡ u ⋅ sec 2 ⁡ u d u

L = 8 ∫ 0 arctg ⁡ 2 sec 3 ⁡ u d u

Agora vamos aplicar a seguinte redução de integrais:

∫ sec n ⁡ u d u = sec n - 1 ⁡ u sen ⁡ u n - 1 + n - 2 n - 1 ∫ sec n - 2 ⁡ u d u

Nossa equação vai ficar:

L = 8 sec 3 - 1 ⁡ u sen ⁡ u 3 - 1 + 3 - 2 3 - 1 ∫ 0 arctg ⁡ 2 sec 3 - 2 ⁡ u d u

L = 8 sec 2 ⁡ u sen ⁡ u 2 0 arctg ⁡ 2 + 1 2 ∫ 0 arctg ⁡ 2 sec ⁡ u d u

A integral da secante é:

∫ sec ⁡ u d u = ln ⁡ tg ⁡ u + sec ⁡ u

Então:

L = 8 sec 2 ⁡ u sen ⁡ u 2 0 arctg ⁡ 2 + 1 2 ln ⁡ tg ⁡ u + sec ⁡ u 0 arctg ⁡ 2

L = 8 2,2361 2 0,8944 2 - 1 2 0 2 + 8 2 ln ⁡ 2 + 2,2361 - ln ⁡ 0 + 1

L = 23,663

Passo 2

E x - é a distância perpendicular do eixo de revolução ao centroide da área de geração. A fórmula para calcular essa distância é:

x - = ∫ L x ~ d L ∫ L d L

Substituindo d L e ∫ L d L que calculamos no passo anterior:

x - = ∫ 0 16 x 1 + x 2 64 d x 23,663

Vamos usar a técnica de substituição:

u = 1 + x 2 64

e

d u = x 32 d x

32 d u = x d x

Os limites de integração vão ficar:

Para x = 0

u = 1 + 0 2 64

u = 1

E para x = 16 :

u = 1 + 16 2 64

u = 1 + 4

u = 5

Subtituindo na integral:

x - = ∫ 1 5 u 32 d u 23,663

x - = 2 3 u 3 / 2 ⋅ 32 23,663 1 5

x - = 0,901 u 3 / 2 1 5

x - = 0,901 5 3 / 2 - 0,901 1 3 / 2

x - = 9,178   m

Passo 3

Então é só aplicar na formula e obteremos a área:

A = θ x - L

A = 2 π 9,178 23 , 6 67

A = 1 365   m 2

Resposta

A = 1365   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

86- Os dois arcos circulares AB e BC são girados em torno do eixo vertical, para se obter a superfície de revolução mostrada. Calcule a área externa A dessa superfície.
91- A área sombreada é limitada por meio ciclo de uma onda senoidal e pelo eixo da onda. Determine o volume gerado por uma revolução completa da área em torno do eixo x .
87- Uma casca fina, mostrada em seção, tem sua forma gerada pela revolução do arco por 360 em torno do eixo z . Determine a área superficial A de um dos dois lados da casca.
94- Para dar sustentação suficiente para o arco de blocos de pedra projetado como mostrado, é necessário conhecer seu peso total W . Use os resultados do Prob. 5 / 11 e determine W . A massa específic
93- Calcule a massa m de concreto necessária para construir a represa em arco mostrada. O concreto tem uma massa específica de 2.4M g / m 3