Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 1
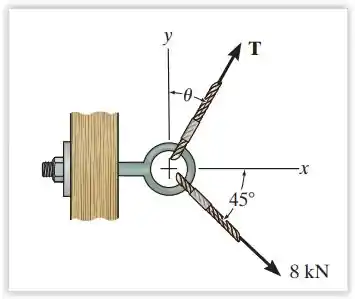
Se e , determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido horário a partir do eixo x positivo.
Passo 1
O problema pede para achar a intensidade e a direção (ângulo) da força resultante, para fazer isso vamos resolver essa questão decompondo as duas forças nos eixos e . Dessa forma ficará mais fácil de trabalhar.
Passo 2
Vamos decompor primeiro a força de :
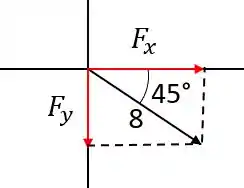
Pela geometria a gente pode verificar que:
E
Dessa forma:
E
obs: Deu o mesmo resultado porque o cosseno e seno de 45° são iguais! Outra coisa, a força em deu negativa porque está no sentido negativo do eixo
Passo 3
Agora vamos decompor a nossa força :
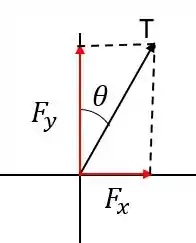
Novamente por geometria a gente verifica:
Dessa forma, substituindo os valores fornecidos na questão:
Passo 4
Agora, como temos as forças decompostas é só somar as componentes verticais e horizontais de cada uma representadas pela força resultante :
Para :
Passo 5
Mas a gente só achou as componentes e não é isso que o problema pede, o problema pede o módulo e o ângulo. Então a gente vai ter que voltar pra geometria, olha como que fica:
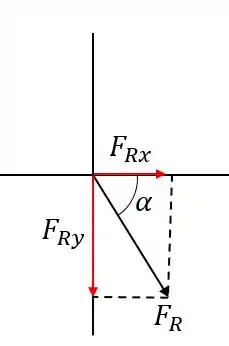
Repara que a força resultante é a hipotenusa do triângulo retângulo, logo:
Agora falta só o ângulo, que no caso é o ângulo , se a gente pegar o seno de por exemplo vamos ter: