Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 3
2.3. Se a intensidade da força resultante deve ser direcionada ao longo do eixo x positivo, determine a intensidade da força T que atua sobre a argola e seu ângulo θ.
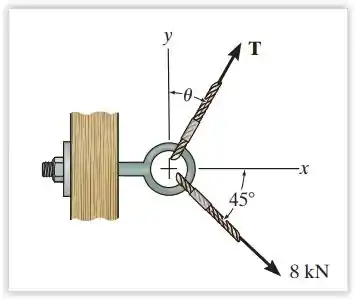
Passo 1
O problema pede para achar a intensidade de força e o ângulo , para fazer isso vamos resolver essa questão decompondo as duas forças nos eixos e . Dessa forma ficará mais fácil de trabalhar.
Passo 2
Vamos decompor primeiro a força de :
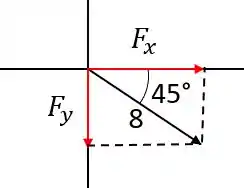
Pela geometria a gente pode verificar que:
E
Dessa forma:
E
obs: Deu o mesmo resultado porque o cosseno e seno de 45° são iguais!
Passo 3
Agora vamos decompor a nossa força :
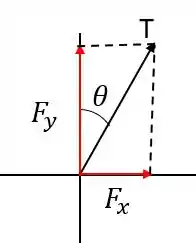
Novamente por geometria a gente verifica:
Passo 4
Agora que é o pulo do gato MIAUUU!!
Como o problema quer uma força que esteja ao longo de eixo então a componente em deve ser zero, desta forma a soma das componentes, em , da força de e da força devem se anular, logo:
obs: Perceba que elas tem direções opostas então se elas se igualarem em módulo, por serem apostas se anularão.
Agora só falta somar as partes em (que tem o mesmo sentido, por isso a soma) e igualar ao valor que o problema pede, :
Viu que temos um sistema?
Agora é só resolver esse sistema.
Passo 5
Resolvendo:
A maneira mais prática de resolver esse tipo de sistema é dividir uma equação pela outra para achar a tangente:
Vamos dividir a primeira pela segunda e achar:
Agora é só substituir em qualquer uma das duas: