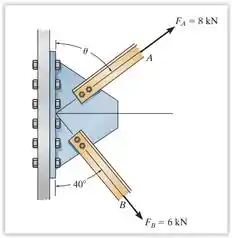
Determine o ângulo de θ para conectar o membro A à chapa de modo que a força resultante de e seja direcionada horizontalmente para a direita. Além disso, informe qual é a intensidade da força resultante.
Passo 1
Gurizadaa, vamos analisar os vetores, extendendo-os para formar um paralelogramo para facilitar os cálculos vem comigo ;)
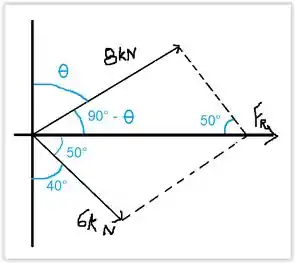
Notem que facilmente pummmm surge um triangulo ahaha, vamos extrai-lo para calcular ;)
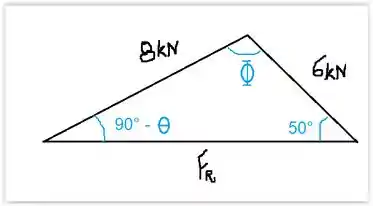
Passo 2
Vamos usar a lei dos senos para calcular , que nada mais é que determinar que em um triângulo qualquer, a relação do seno de um ângulo é sempre proporcional à medida do lado oposto a esse ângulo, vejam comigo ;)
Lembre-se que temos que pegar o valor e dividir pelo extremo oposto, tipo sen50 o oposto é 8KN, e assim por diante...
Agora vamos isolar “teta” para achar o valor do ângulo
Passo 3
Agora vamos usar a lei dos cossenos (é utilizada para calcular a medida de um lado ou de um ângulo desconhecido de um triângulo qualquer, conhecendo suas outras medidas. ).
Vamos determinar esse com a propriedade que diz que a soma dos ângulos internos de um triângulo é .
Então
Acabouuuu gurizadaaaaa!!!!!!!!!