Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 23
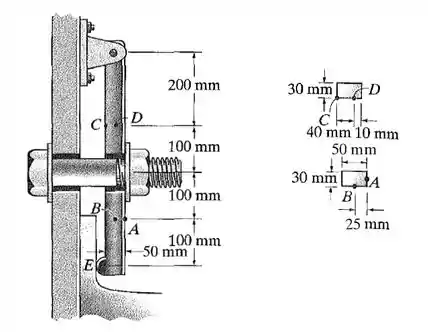
23. Resolva o Problema 9.22 para os pontos C e D.
Passo 1
Primeiro, vamos calcular as forças de reações no pino e no ponto .
Fazendo a soma de momentos em relação a pino e considerando o sentida anti-horário como sendo positivo:
E agora, fazemos a soma de forças no eixo , chamando a reação no pino de e considerando o sentido da direita como positivo:
Passo 2
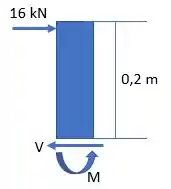
Agora, faremos a análise dos esforços cortantes e momentos fletores a partir do pino e com o corte no ponto (ou ):
Passo 3
Neste passo, iremos calcular o momento de inércia da seção transversal. Sabemos que para seções retangulares, temos a seguinte equação de momento de inércia:
Onde é o tamanho da parede paralela ao eixo e é o tamanho da parede perpendicular ao eixo:
Passo 4
Como nossos cálculos são comuns aos dois pontos, iremos dividir a questão, resolvendo primeiro que foi pedido para o ponto e depois para o ponto .
Cálculo da tensão no ponto :
Cálculo da tensão máxima de cisalhamento no ponto :
Passo 5
Calcularemos, então, as tensões principais no ponto :
Logo, obtemos duas tensões e :
Passo 6
Fazendo as contas para o ponto , temos:
Cálculo da tensão no ponto D:
Cálculo da tensão máxima de cisalhamento no ponto :
Passo 7
E agora, vamos pro cálculo das tensões principais no ponto :
Novamente obtemos duas tensões, e :
Passo 8
Calcularemos, agora, o ângulo que o elemento será rotacionado, com os resultados lá do
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Para achar o outro, devemos somar noventa graus com o nosso ângulo :
Resposta
As tensões principais no ponto são:
E as tensões no ponto são:
