Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 27

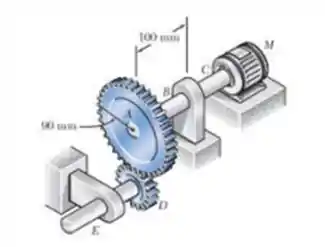
O eixo de seção cheia ABC e as engrenagens mostradas na figura transmitem 10   k W do motor M para uma máquina-ferramenta conectada à engrenages D . Sabendo que o motor gira 240   r p m e que τ a d m = 60   M P a ,determine o menor diâmetro admissível para o eixo ABC.

Passo 1

E ai gurizada tudo beleza? O enunciado pede que a gente determine o menor diâmetro admissível para o eixo ABC. Vamos as conversões, partiu!

f = 240   r p m 60 s e c / m i n = 4   H z

T = P 2 π f = 10 × 10 3 ( 2 π ) ( 4 ) = 397,89   N ⋅ m

Passo 2

Considere o esboço da engrenagem abaixo :D

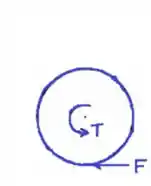
Engrenagem A: F r A - T = 0

F = T r A = 397,89 90 × 10 - 3 = 4421   N

Momento de flexão em B:

M B = L A B F = ( 100 × 10 - 3 ) ( 4421 ) = 442,1 N ⋅ m

τ a l l = c J M 2 + T 2

Passo 3

Agora sim podemos determinar o diâmetro, vem comigo :D

J c = π 2 c 3 = M 2 + T 2 τ a l l

c 3 = 2 π M 2 + T 2 τ a l l = ( 2 ) 442,1 2 + 397,89 2 π ( 60 × 10 6 ) = 6,3108 × 10 - 6 m 3

c = 18,479 × 10 - 3 m d = 2 c = 37,0 × 10 - 3 m

d = 37,0   m m

Resposta

37 mm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38. Resolva o Problema 9.36 para o ponto C localizado no centro na superfície inferior da alma.
37. Resolva o Problema 9.36 para o ponto B.
O parafuso está preso a seu suporte em C. Se aplicarmos uma força de 90 N à chave para apertá-lo, determine as tensões principais desenvolvidas na haste do parafuso no ponto A. Represente os resultado
40. Resolva o Problema 9.39 para o ponto B localizado na alma na parte superior da aba inferior.
39. A viga de abas largas está sujeita à força de 50k N . Determine as tensões principais na viga no ponto A localizado na alma na parte inferior da aba superior. Embora a precisão não seja muito boa,