Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 23
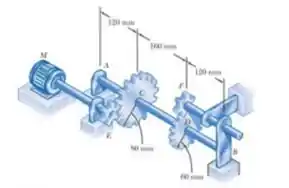
O eixo de seção cheia AB rotaciona a e transmite a partir do motor M para a máquina-ferramentas conectadas à engrenagem F.Sabendo que ,determine o menor diâmetro permitido para o eixo AB.
Passo 1
Muito bem gurizada, vamos começar nossos cálculos? Considere o esboço ;)
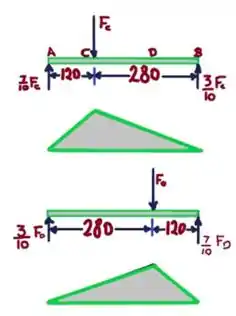
Então partiu determinar a frequência e o torque ;)
Passo 2
Na engrenagem C:
Na Engrenagem D:
Força no plano vertical:
Passo 3
Força no plano horizontal:
Em C:
Em D:
Resposta
57.
Exercícios de Livros Relacionados
34. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A. Os mancais suportam apenas reações ve
31. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvida em qualquer lugar na superfície do eixo.
30. A viga de abas largas está sujeita às cargas mostradas. Determine a tensão principal na viga no ponto A e no ponto B. Esses pontos estão localizados na parte superior e na parte inferior da alma,
35. O tubo da perfuratriz tem diâmetro externo de 75m m , espessura de parede de 6m m e pesa 0,8k N / m . Se for submetido a um torque e a carga axial como mostra a figura, determine:(a) as tensões pr
36. As cargas internas em uma seção da viga são mostra das na figura. Determine as tensões principais no ponto A. Calcule também a tensão de cisalhamento máxima no plano nesse ponto