Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 24

Resolva o Prob. 8.23 assumindo que o eixo AB rotacionado a 720   r p m

Passo 1

Muito bem gurizada, vamos começar nossos cálculos?! Vejam o esboço comigo, partiu!!!

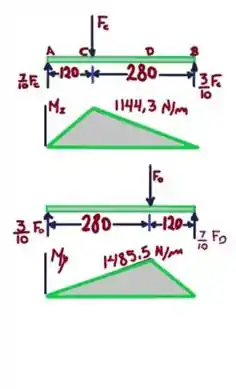
Definindo a frequência e o torque respectivamente temos:

f = 720   r p m 60 s e c / m i n = 12 H z

T = P 2 π f = 80 × 10 3 ( 2 π ) ( 10 ) = 1061,03   N / m

Passo 2

Na Engrenagem C:

F C = T r C F C = 1061,03 80 × 10 3 = 13.2629 × 10 3   N

Passo 3

Na Engrenagem D:

F D = T r D F D = 1061,03 60 × 10 3 = 17,6838 × 10 3 N

Força no plano vertical:

M C z = 120 × 10 3 7 10 F c = 1114,08   N / m

M D z = 120 280 M C z = 477,46   N / m

Passo 4

Força no plano horizontal:

M D y = 120 × 10 3 7 10 F D = 1485,44   N / m

M C y = 120 280 M D y = 636,62   N / m

Em C:

M Y 2 + M Z 2 + T 2 = 1665,01   N / m

Em D:

M Y 2 + M Z 2 + T 2 = 1886,87   N / m

Passo 5

Agora devemos a partir da equação da tensão de cisalhamento determinar o diâmetro, vem comigo que falta pouco ;)

τ a d m = c J M Y 2 + M Z 2 + T 2 m a x

J c = π 2 c 3 = M Y 2 + M Z 2 + T 2 < m a x τ a d m = 1886,87 60 × 10 6 = 31,448 × 10 - 6   m 3

c = 27,1 53 × 10 - 3 m

d = 2 c = 54.3 × 10 - 3 = 54.3   m m

Resposta

54.3   m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46. O tubo de aço tem diâmetro interno de 68m m e diâmetro externo de 75m m . Se estiver preso em C e for submetido à força horizontal de 100N que age na extremidade do cabo da chave, determine as ten
43. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais desenvolvidas no ponto A e no ponto B , localizado imediatamente à esquerda da carga de
50. Uma barra tem seção transversal circular com diâmetro de 25m m e está sujeita a torque e a momento fletor. No ponto de tensão de flexão máxima as tensões principais são 140M P a e - 70M P a . Dete
49. A viga-caixão está sujeita às cargas mostradas na figura. Determine as tensões principais na viga no ponto A e no ponto B .
51. As cargas internas em uma seção da viga consistem em uma força axial de 500N , uma força de cisalhamento de 800N e duas componentes de momento 30N ⋅ m e 40N ⋅ m . Determine as tensões principais n