Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 97
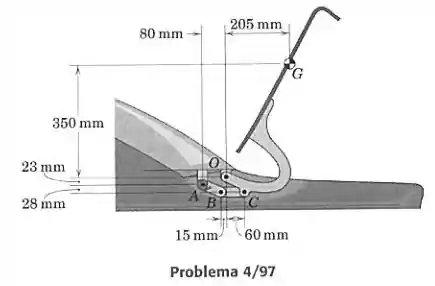
Os elementos de um mecanismo acionados por uma mola, da tampa do porta-malas de um carro, estão mostrados na figura. Para a posição de equilíbrio mostrada, determine o momento que cada uma das molas de torção em deve exercer sobre a conexão . A massa da tampa do porta-malas é de 18 kg, com centro de massa em . Os efeitos dos pesos dos outros elementos podem ser desprezados.
Passo 1
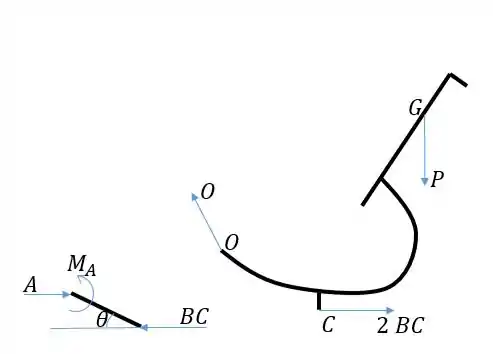
Vamos primeiro entender o que está acontecendo no problema, para sabermos onde aplicar as condições de equilíbrio. A conexão tem tendência de girar em torno de por conta da força causada pelo elemento no ponto . Por outro lado, o corpo que possui a tampa tem a tendência de girar no sentido horário por conta do peso da tampa, mas é impedido pela força causada por e pela reação em . Na verdade, temos 2 conexões diferentes (uma de cada lado do carro) que seguram a tampa, então no diagrama que fizermos mostramos . Vamos então isolar em diagrama de corpo livre essas duas partes:
Passo 2
Primeiro vamos achar , fazendo o momento em torno de . As distâncias das forças até o ponto são dadas no desenho do enunciado, e consideramos g = 9,81 m/s²:
Passo 3
Agora encontramos fazendo o momento em torno de na conexão . A distância vertical de até é dada e igual a 28 mm. Temos em na verdade
Substituindo pelo valor de que já encontramos, resolvemos a questão: