Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 100

Determine a força de aperto vertical em E em termos da força P aplicada ao cabo do rebitador.

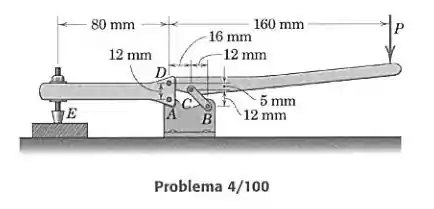
Passo 1

Vamos isolar nossos corpos de interesse em diagramas de corpo livre, mostrando as forças que atuam neles:

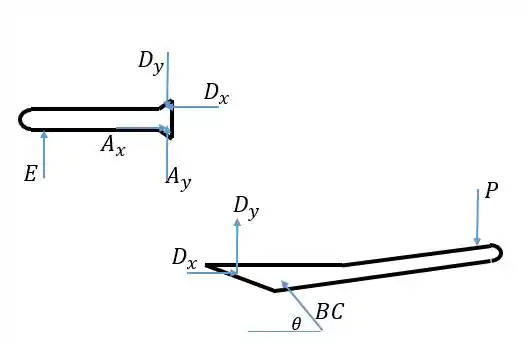
Passo 2

Podemos encontrar E fazendo para o corpo da esquerda o momento em torno de A , mas para isso precisamos de D x que é a única incógnita além de E que aparece nessa conta. Vamos então encontrar D x através das equações de equilíbrio para o corpo da direita. Primeiro encontramos B C através do momento em torno de D . Precisamos do ângulo θ que B C faz com a horizontal:

tg ⁡ θ = 12 12 = 1 ⇒ θ = 45 °

As distâncias são dadas pelo desenho do enunciado. Note que a componente horizontal de B C causa um momento horário e a componente horizontal um momento anti-horário. Então:

∑ M D = 0 ⇒ - P 160 - B C cos ⁡ 45 ° 5 + B C sen ⁡ 45 ° 16 = 0

⇒ - 160 P - 5 2 2 B C + 16 2 2 B C = 0

⇒ - 160 P + 11 2 2 B C = 0

⇒ 11 2 2 B C = 160 P

⇒ B C = 320 P 11 2

Passo 3

Agora que temos B C , acharemos D x fazendo ser zero a soma das forças horizontais para esse corpo:

∑ F x = 0 ⇒ D x = B C cos ⁡ 45 ° = 320 P 11 2 × 2 2

⇒ D x = 160 P 11

Passo 4

Finalmente agora olhando para o corpo da esquerda, podemos encontrar E usando o valor de D x e fazendo o momento em torno de A :

∑ M A = 0 ⇒ D x 12 - E 80 = 0

⇒ 80 E = 12 D x ⇒ E = 12 80 D x = 3 20 D x

Substituindo o valor de D x :

E = 3 20 × 160 P 11

⇒ E = 24 P 11

Resposta

E = 24 P 11

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

61.Se a tração no cabo é F = 700N , determine a intensidade do momento produzido pela força em relação ao eixo da dobradiça, CD, necessária para manter o painel na posição mostrada.
66. A chave de boca articulável está sujeita a uma força de P = 80N , aplicada perpendicularmente ao cabo, como mostra a figura. Determine o momento ou torque isso opõe ao longo do eixo vertical do pa
67. Se um torque ou momento de 10N ⋅ m é necessário para afrouxar o parafuso em A, determine a força P que precisa ser aplicada perpendicularmente ao cabo da chave de boca articulada.
63. A estrutura na forma de um A está sendo suspensa para uma posição ereta pela força vertical F = 400N . Determine o momento dessa força em relação ao eixo y’ passando pelos pontos A e B quando a es
65. A estrutura na forma de um A está sendo suspensa para uma posição ereta pela força vertical F = 400N . Determine o momento dessa força em relação ao eixo y quando a estrutura está na posição mostr