Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas fundamentais - Ex. 6
Determine a força em cada membro da treliça. Indique se os membros estão sob tração ou compressão.
Passo 1
O problema que que a gente encontre a força de cada treliça mostrando se ele está sendo tracionada ou comprimida.
Vamos começar procurando os membro de força zero (se existem), lembra das regrinhas? Vou te lembrar:
Caso em que existam duas barras colineares e uma terceira conectada, essa terceira barra é um membro de força zero:
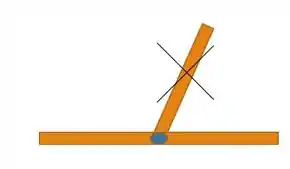
Caso em que existam uma barra colinear a uma força e uma segunda barra conectada, essa barra é um membro de força zero:
Caso em que um nó na extremidade, e nesse nó exista apenas duas barras chegando, essas duas barras são membros força zero, a não ser que exista forças atuando sobre o nó. membros força zero:
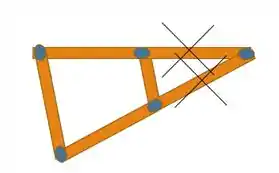
Usando essas regras, a gente descobre que e consequentemente .
E como , então .
Portanto e estão ligados ao apoio e não estão recebendo forças, então não possuem forças de reação, ou seja:
Passo 2
Agora, vamos fazer um diagrama de corpo livre no ponto , e já sabemos que não exerce força, então fica:
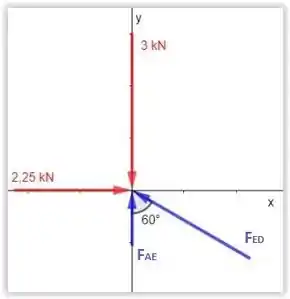
Passo 3
Com isso a gente calcula as forças , , pois sabemos que o somatório das forças no eixo e somatório das forças do eixo é .
Então temos que:
E como vimos no passo 1 , então:
Que por fazerem uma força de reação nesse sentido, estão sob compressão.
Agora no eixo :
E assim encontramos:
Que por fazer uma força de reação nesse sentido, está sob compressão.
Passo 4
Por fim, a gente analisa os pontos :
Analisamos na horizontal:
Temos assim que esses membros encontramsse tracionadas.
Resposta
(Compressão)
(Compressão)
(Tração)