Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 49
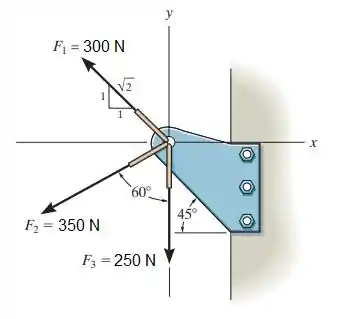
2.49. Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Passo 1
Falaaa
O exercício pede para a gente determinar a intensidade e a direção de . Para isso vamos decompor as forças em termos dos eixos x e y para facilitar os cálculos, aí poderemos determinar a componente da força resultante no eixo x e depois a componente no eixo y e soma-las vetorialmente.
Bora!
Passo 2
Vamos começar por .
Repare que não temos um valor de ângulo explicito, mas a figura nos dá esse triângulo
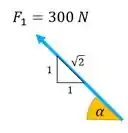
Aí para achar a componente de , como o nosso ângulo está colado em , a gente multiplica a nossa força por cosseno
A gente coloca o sinal de menos porque nossa força está no sentido negativo de . E fica com seno, mas positivo, porque a força está no sentido positivo de :
Aí escrevendo na forma vetorial temos:
Vamos olhar a figura e lembrar que
E
Então, sabendo que
Passo 3
Agora vamos determinar . O ângulo de está coladinho em , então essa componente vai ficar com cosseno e outra com seno desse ângulo. E a força está apontando para o sentido negativo dos dois eixos, então as componentes ficam:
Na forma vetorial
E por fim está somente na direção de , no sentido negativo, aí essa vai ser a sua única componente:
Aí vetorialmente
Passo 4
Agora podemos determinar . Vamos somar todos os vetores que a gente achou componente a componente
Daí
Agora vamos calcular a intensidade de
Passo 5
Vamos representar vetorialmente a situação
Repare que da representação vetorial podemos extrair o seguinte triângulo
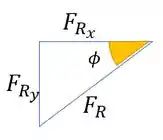
E para determinar , basta lembrar que
Então
Então para determinar o ângulo em relação ao sentido anti-horário do eixo x positivo vamos usar
