Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 81
Determine a força de fixação exercida no bloco se uma força é aplicada na manivela da morsa. O parafuso de rosca quadrada simples tem um diâmetro médio de e um passo de . O coeficiente de atrito estático é .
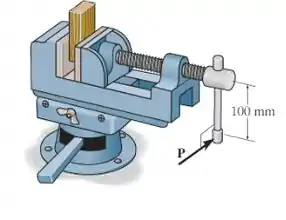
Passo 1
Galera, para um parafuso de rosca quadrada, o ângulo de passo é determinado a partir de . Aqui, é o passo da rosca e é o raio médio da rosca. Tendo essa ideia em mente, vamos calcular o ângulo de passo da nossa questão:
Passo 2
O ângulo de atrito estático para o parafuso de rosca quadrada é dado por . Logo,
Passo 3
Vamos dizer que . Assim, a equação para o momento do parafuso é dada por:
Substituindo os valores na equação, temos:
Resposta
A força de fixação é igual a:
Exercícios de Livros Relacionados
131- O cilindro tem massa de 36k g e a barra esbelta uniforme a ele presa tem uma massa m desconhecida. Esse conjunto permanece em equilíbrio estático para valores do ângulo θ de até 45 , mas escorreg
O parafuso de rosca quadrada do grampo tem um diâmetro médio de 14m m e um passo de 6m m . Se μ s = 0,2 para as roscas e o torque aplicado na alça é de 1,5N . m , determine a força compressiva F sobre
Determine a menor força horizontal P exigida para mover o calço para a direita. O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0,3 . Faça θ = 15 ° e F = 400N . Despreze o
Os blocos de calço são usados para manter a amostra em uma máquina de teste de tração. Determine o maior ângulo de projeto θ dos calços de modo que a amostra não deslize independente da carga aplicada
Se o bloco de concreto uniforme tem uma massa de 500k g , determine a menor força horizontal P necessária para mover o calço para a esquerda. O coeficiente de atrito estático entre o calço e o concret