Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 80

Uma carga central P deve ser suportada pela barra de aço AB. Usando método de tensão admissível, determine a menor dimensão d da seção transversal que pode ser usada quando:

(a) P   =   108   k N ,

(b) P   =   166   k N

Use 250   M P a e E   =   200   G P a

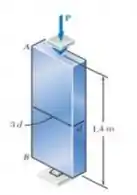
Passo 1

Então gurizada, vamos começar nosso cálculos?!

Transição: L e r : 4,71 E σ Y = 4,71 200 × 10 9 250 × 10 6 = 133,22

L e = L = 1,4   m   A = ( 3 d ) ( d ) = 3 d 2 I = 1 12 ( 3 d ) ( d ) 3 = 1 4 d 4

r = I A = d 12 = 0,288675 d

Passo 2

(a) P = 108 × 10 3   N Presume-se L e r > 133,22

P a l l = 0,877 π 2 E I 1,67 I = ( 1,67 ) P a l l L E 2 0,877 π 2 E = 1 4 d 4

d 4 = ( 4 ) ( 1,67 ) P L E 2 0,877 π 2 E = ( 4 ) ( 1,67 ) ( 108 × 10 3 ) 1,4 2 ( 0,877 π 2 ) ( 200 × 10 9 ) = 816 × 10 - 9     m 4

d = 30,063 × 10 - 3   m r = 8,678 × 10 - 3 m

L e r = 1,4 8,678 × 10 - 3 = 161,32 > 133,22

d=30,1 mm

Passo 3

(b) P = 166 × 10 3 N Presume-se L e r > 133,22

d 4 = ( 4 ) ( 1,67 ) ( 166 × 10 3 ) 1,4 2 ( 0,877 π 2 ) ( 200 × 10 9 ) = 1,25548 × 10 - 9   m 4

d = 33,474 × 10 - 3   m r = 9,663 × 10 - 3 m

L e r = 1,4 9,663 × 10 - 3 = 144,88 > 133,22

d=33,5 mm

Resposta

Muito bem turminha, depois de nossos cálculos, chegamos ao nosso resultados: temos em (a): d = 30,1   m m ; e em (b) temos d = 33,5   m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

24. A treliça é feita de barras de aço A - 36 e cada uma delas tem seção transversal circular com diâmetro de 40m m . Determine a força máxima P que pode ser aplicada sem provocar flambagem em nenhuma
18. A coluna de tubo de aço A - 36 de 3,6m m tem diâmetro externo de 75m m e espessura de 6m m . Determine a carga crítica, se considerarmos que suas extremidades estão acopladas por pinos.
19. A coluna de tubo de aço A - 36 de 3,6m m tem diâmetro externo de 75m m e espessura de 6m m . Determine a carga crítica, se a base estiver engastada e o topo preso por pinos.
20. A coluna retangular de madeira de 3 m tem as dimensões mostradas na figura. Determine a carga crítica, se considerarmos que as extremidades estão acopladas por pinos. E m = 12G P a , σ e = 35M P a
21. A coluna de 3,0m tem as dimensões mostradas na figura. Determine a carga crítica, se a base for engastada e o topo estiver preso por pinos. E m = 12G P a , σ e = 35M P a .