Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 31

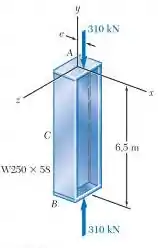
A linha de ação da força axial de 310   k N é paralela ao eixo geométrica da coluna AB e intercepta o eixo x   em x = e .   Usando E = 200 G P a , determine (a) a excentricidade e quando a deflexão no ponto médio C da coluna for 9 mm e (b) a tensão máxima na coluna

Passo 1

E ai gurizada tudo belezaaaaa? O enunciado pede que a gente, determine a excentricidade e quando a deflexão no ponto médio C da coluna for 9 mm e a tensão máxima na coluna

Para uma seção W250 x 58, A = 7420   m m 2 = 7420 × 10 - 6 m 2 temos os seguintes dados:

I y = 18,7 × 10 6 m m 3 = 18,7 × 10 - 6 m 4

S y = 185 × 10 3 m m 3 = 185 × 10 - 6 m 3

L = 6,5 m           L e = 6,5 m

Vamos começar calculando a força P vem comigo :D

P c r = π 2 E I L e 2 = π 2 200 × 10 9 18,7 × 10 - 6 6,5 2 = 873,7 × 10 3 N

P P c r = 310 × 10 3 873,7 × 10 3 = 0,35483

Passo 2

Agora partiu determinar a excentricidade e quando a deflexão no ponto médio C da coluna for 9 mm :D

y m a x = e   s e c π 2 P P c r - 1 = 0,68558 e

  1. e = y m a x 0,67990 = 9 × 10 - 3 0,67990 = 13,13 × 10 - 3 m = 13,13 m m

Passo 3

Por último e não menos importante determinar a tensão máxima na coluna, mas antes devemos determinar o momento máximo :D

M m a x = P e + y m a x = 310 × 10 3 9 + 13,13 ) 10 - 3 = 6859,6 N ∙ m

σ m a x = P A + M c I = P A + M S y = 310 × 10 3 7420 × 10 - 6 + 6859,6 185 × 10 - 6 = 41,78 × 10 6 + 37,08 × 10 6 = 78,86 × 10 6 P a = 78,9 M P a

Resposta

  1. 13,13 m m
  2. 78,9 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pede-se: (a) considerando somente flambagem no plano da estrutura mostrada, e usando a fórmula de Euler, determinar o valor de θ entre 0° e 30° determinar o fator de segurança
Uma coluna de 4m de comprimento efetivo deve suportar uma carga centrada de 800kN. Sabendo que σ e = 250M P aeE = 200 G P a e usando as fórmulas da AISC, selecionar o perfil laminado de abas largas de
Resolver a parte b do Prob. Resolvido 11,2, assumindo que a carga axial P é aplicado com uma excentricidade e = 20 m m , em um ponto localizado sobre uma das diagonais da seção transversal do tubo est
Uma carga axial de 60kN será aplicada com uma excentricidade e = 8mm em uma barra circular de aço BC, que está livre em seu topo C e engastada em sua base B. Sabendo-se que as barras disponíveis para
Um tubo de alumínio de de 75 mm de diâmetro externo e 2m de comprimento efetivo, deve suportar uma carga centrada de 95k N . Sabendo-se que os tubos disponíveis para o uso são feitos da liga 6061 - T