Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 127

Uma carga vertical P de é aplicada no ponto médio de uma aresta da seção transversal quadrada de um elemento de aço comprimido AB,o qual é livre no topo A e fixo em sua base B . Sabendo que para o grau de aço utilizando de aço utilizando e utilizando o método das tensões admissíveis,determine a menor dimensão d admissível.

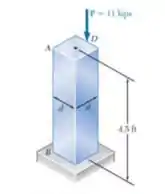
Passo 1

E aí gurizada, esse vai ser um pouco longo, mas nada que não podemos resolver não é?! vamos começar logo?! iniciemos:

Aço: ksi

Transição:

assumindo >133,68 de modo que

e

seção transversal quadrada:

para todos os eixos através do centro do quadrado.

Passo 2

Tensão admissível para carregamento centralizado.

Carregamento excêntrico:

quando o carregamento está no ponto D.

Método de estresse permitido:

Passo 3

Equacionando as duas expressões para :

Suposição verificada

Menor dimensão permitida

Resposta

.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão de 3m de comprimento efetivo é feito, parafusando-se juntos dois perfis laminados de aço L102x76x6,4, como mostrado. Sabendo-se que σ e = 250M P aeE = 200 G P a , determinar a

Uma barra de 9,5mm de diâmetro, feita de liga de alumínio 6061-T6 é usada como uma coluna. Determinar a carga centrada admissível para coluna, quando o comprimento efetivo for: (a) 7000 mm;(b)3000mm.

Resolver o problema 11.135 usando o método da interação.

Usando a liga de alumínio 2014-T6, determinar o maior diâmetro admissível da barra de alumínio AB para uma carga centrada P de intensidade igual a: (a) 108 kN; (b) 166 kN

Resolver o Prob. 11.132, usando o método da interação, para uma carga de intensidade P = 80k N e uma tensão admissível na flexão de 150 kN.