Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 26
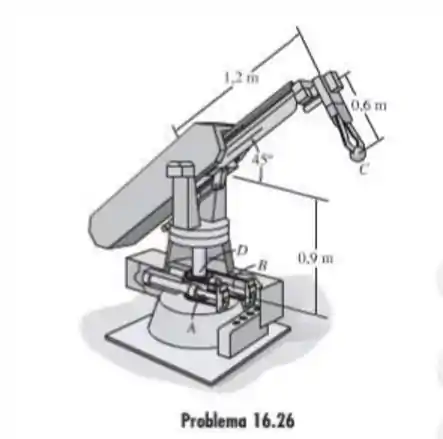
26. A rotação do braço robótico ocorre em virtude do movimento linear dos cilindros hidráulicos A e B. Se esse movimento faz com que a engrenagem D gire no sentido horário a 5 rad/s, determine a intensidade da velocidade e aceleração da peça C segura pelas garras do braço.
Passo 1
Falaa pessoal tudo certinho? Vamos começar fazendo um desenho e observando o ponto C em relação a engrenagem D, que é o que importa pra gente encontrar a velocidade e aceleração em C.
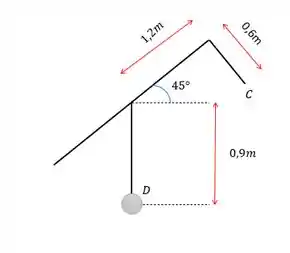
E aqui vamos definir também alguns parâmetros.
velocidade angular da engrenagem D é
E como o braço do robô está preso à engrenagem, temos
Passo 2
A velocidade pode ser encontrada partir da geometria. Temos a distância da peça C do eixo rotativo como
A magnitude da velocidade da peça C é expressa como
Nesse sentido, temos
A magnitude da velocidade da peça C é
Passo 3
O componente tangencial da aceleração da parte C é expresso como
Nesse sentido, temos
O componente normal da aceleração da parte C é expresso como
Nesse sentido, temos
A magnitude da aceleração da parte C é expressa como
Nesse sentido, temos
A magnitude da aceleração da peça C é .