Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 27

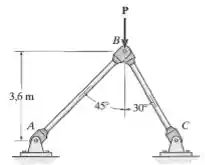
27. O mecanismo articulado é composto por duas hastes de aço A - 36 , cada uma com seção transversal circular. Determine, com aproximação de múltiplos ele 5   m m , o diâmetro de cada haste que suportará uma carga   P   =   30   k N . Considere que as extremidades das hastes estão acopladas por pinos. Use fator de segurança de 1,8 para flambagem.

Passo 1

Primeiro, vamos montar o diagrama de forças para o ponto B :

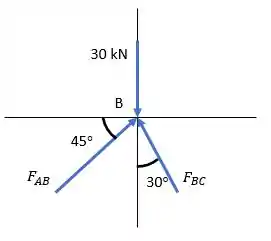
E fazer o somatório de forças:

↑ + ∑ F y = 0 → - 30   k N + F A B c o s 45 ° + F B C c o s ( 30 ° ) = 0

3 2 F B C = 30   k N - F A B 2 2

F B C = 2 3 30   k N - F A B 2 2

∴ F B C = 60 - 2 F A B 3   ( I )

→ + ∑ F x = 0 → F A B s e n 45 ° - F B C s e n ( 30 ° ) = 0

1 2 F B C = 2 2 F A B

∴ F B C = 2 F A B   ( I I )

Igualando as equações ( I ) e ( I I ) :

2 F A B = 60 - 2 F A B 3   → 6 F A B = 60 - 2 F A B

6 F A B + 2 F A B = 60   k N → ( 6 + 2 ) F A B = 60   k N

F A B = 60   k N 6 + 2

∴ F A B = 15,5   k N

F B C = 2 ⋅ 15,5   k N

∴ F B C = 21,96   k N

Passo 2

Conhecida as forças em ambas hastes, vamos calcular primeiro a carga máxima para que não haja flambagem na haste A B e depois para a haste B C .

P c r = π 2 E I ( k L ) 2

Como as extremidades estão presas por pinos, temos k = 1 .

O momento de inércia de uma seção circular, é dado pela fórmula:

I = π 4 r 4

E temos, também, por ser dado no enunciado que é um aço A - 36 :

E = 200 × 10 9   P a

Para o valor de L , faremos:

L = 3,6 c o s ⁡ ( 45 ° )

P c r = π 2 ( 200 × 10 9   P a ) ( π 4 r A B 4   m 4 ) ( 1 × 3,6 c o s ⁡ ( 45 ° )   m ) 2

Mas como temos o fator de segurança:

F . S . = P c r F A B

1,8 = P c r 15,5   k N → P c r = 27,9   k N

27,9   k N = π 2 ( 200 × 10 9   P a ) ( π 4 r A B 4   m 4 ) ( 1 × 3,6 c o s ⁡ ( 45 ° ) m ) 2

r A B 4 = 27,9   k N ( 1 × 5,091   m ) 2 π 2 ( 200 × 10 9   P a ) ( π 4 )   m 4

∴ r A B = 26,15   m m

O diâmetro será o dobro do raio r A B :

d A B = 2 ⋅ r A B = 2 × 26,15   m m

∴ d A B = 52,3   m m   ≅ 55   m m

Passo 3

Vamos calcular a tensão devido à força crítica σ c r para verificar se ele ultrapassa a tensão de escoamento σ e :

σ c r = P c r A

σ c r = 15,5   k N π × 0,0275 2   m 2

∴ σ c r = 6,54   M P a

σ c r = 6,54   M P a < σ e = 250   M P a

Como σ c r < σ e , a carga crítica é admissível elemento.

Passo 4

Como já calculamos o diâmetro para a haste A B , vamo calular o valor do diâmetro para a haste B C . Todos os calculados serão repetidos com a diferença da variável r B C .

P c r = π 2 E I ( k L ) 2

Pelo fator de segurança:

F . S . = P c r F A B

1,8 = P c r 21,96   k N → P c r = 39,53   k N

E o valor de L será:

L = 3,6 c o s ( 30 ° )

39,53   k N = π 2 ( 200 × 10 9   P a ) ( π 4 r A B 4   m 4 ) ( 1 × 3,6 c o s ⁡ ( 30 ° )   m ) 2

r B C 4 = 27,9   k N ( 1 × 4,157   m ) 2 π 2 ( 200 × 10 9   P a ) ( π 4 )   m 4

∴ r B C = 25,76   m m

O diâmetro será o dobro do raio r B C :

d B C = 2 ⋅ r B C = 2 × 25,76   m m

∴ d B C = 51,5   m m   ≅ 50   m m

Passo 5

Finalmente calcular a tensão devido à força crítica σ c r para verificar se ele ultrapassa a tensão de escoamento σ e :

σ c r = P c r A

σ c r = 21,96   k N π × 0,025 2   m 2

∴ σ c r = 11,18   M P a

σ c r = 11,18   M P a < σ e = 250   M P a

Como σ c r < σ e , a carga crítica é admissível elemento.

Resposta

O diâmetro da haste A B para ela suportar uma carga de 30   k N deverá ser:

d A B = 55   m m

E o diâmetro para a haste B C :

d B C = 50   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma coluna com comprimento de flambagem de 5,8m deve suportar uma carga centrada de 310k N e carga externa centrada de 375k N . Sabendo que σ E = 250M P a e E= 200G P a . Utilize o método do coeficien
10.70 Um tubo de alumínio estrutural é reforçado rebitando-se nele duas placas, como mostra a figura, para ser usado como uma coluna de 1,7mm de comprimento de flambagem. Sabendo-se que todo o materia
A coluna laminada colada da figura é feita com quatro pranchas, cada uma com seção transversal de 38 x 190 mm. Sabendo que, para o grau de madeira utilizado, a tensão admissível ajusta para compressão
Uma coluna laminada colada com 2,1m de comprimento de flambagem deve ser feita com tábuas de seção transversal 25 x 150mm. Sabendo que, para o tipo de madeira utilizado, a tensão admissível ajustada à
Uma força centrada de 80,1 kN é aplicada a uma coluna retangular de madeira serrada com 6,71m de comprimento de flambagem. Usando madeira serrada para a qual a tensão admissível ajustada à compressão