Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 8
2.8. Determine a intensidade e a direção da força resultante.
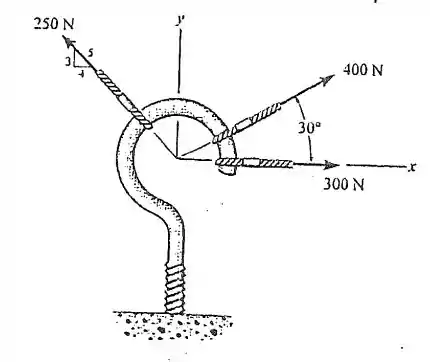
Passo 1
Vamos usar a seguinte estratégia, vamos decompor todos os vetores nos eixos x e y, então ficará mais fácil para a gente calcular as resultantes em x e em y. Uma vez que tivermos a resultante decomposta, basta fazer uma soma vetorial das componentes e finalmente teremos a intensidade da força resultante.
Passo 2
Vamos começar decompondo o vetor de , vamos chama-lo de .
Repare que esse vetor não tem componente no eixo y, então
Agora vamos fazer isso com o vetor de , vamos chamá-lo de
Agora a o vetor de , que vamos chamar de
Esse aqui é um pouquinho mais complicado, por que não temos o ângulo assim de cara, mas a imagem nos dá um triângulo, vamos usá-lo
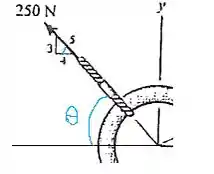
Vamos lembrar que e
Repare também que essa força está no sentido oposto de x, então é negativa
Passo 3
Agora vamos fazer calcular as componentes da nossa resultante
Vamos fazer uma representação vetorial só com a força resultante
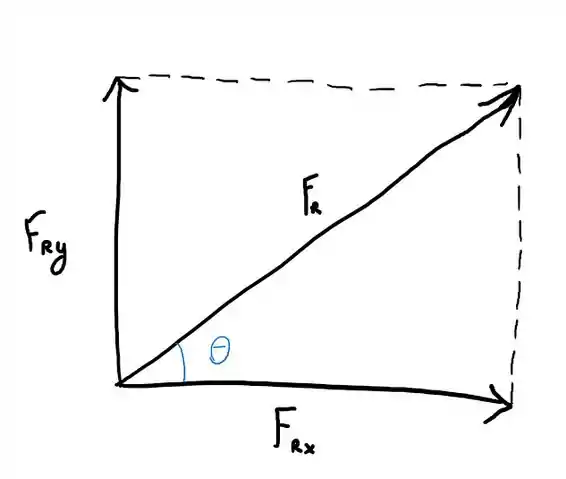
Então vamos fazer a soma vetorial para obter
Passo 4
Agora basta calcular a direção θ
Para isso vamos extrair esse triângulo da nossa representação vetorial
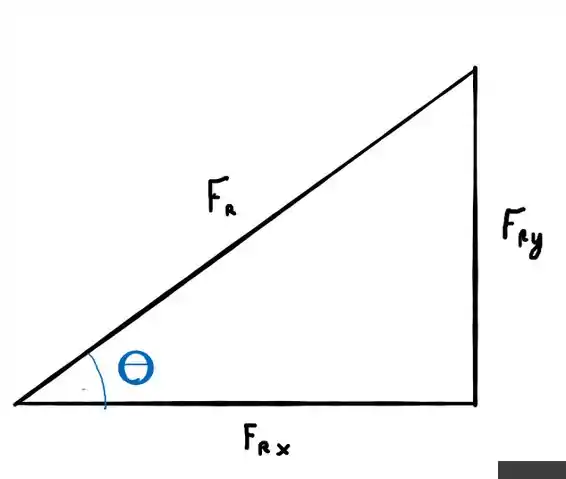
E vamos lembrar que
Então