Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 7
2.7. Decomponha cada força que atua sobre o poste em suas componentes x e y
Passo 1
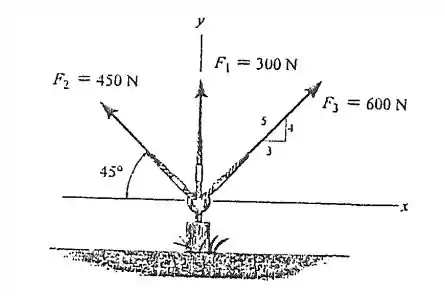
Fala ai galerinha do RespondeAí, tudo beleza? Nesse exercício aqui o enunciado nos fornece forças que atuam sobre um suporte como na figura abaixo:
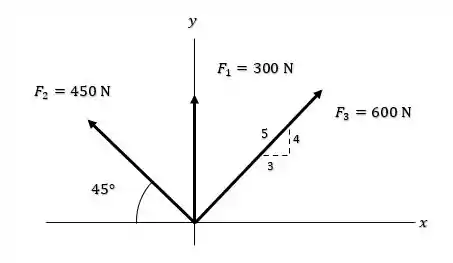
E sabendo disso ele nos pede para encontrar as componentes em cada eixo de cada força que atua no suporte. Bora lá ver como que fica essa brincadeira então.
Passo 2
Primeiro podemos fazer a decomposição para a força , como ele está estritamente no eixo , temos que a componente no eixo é nula:
E temos apenas componente no eixo :
Passo 3
Agora para a força podemos usar a relação com o ângulo de , de modo que no eixo vamos ter que:
Logo
E agora para o eixo , vamos obter que:
O sinal negativo vem do fato da força estar no sentido negativo do eixo .
Passo 4
E agora para a última força , vamos usar a sagacidade de que o ângulo que a força faz com eixo é mesmo do triângulo “345”:
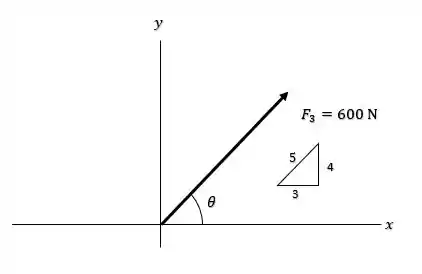
Isso quer dizer que as relações de seno e cosseno serão as mesmas, logo:
Sendo assim, a força pode ser decomposta como:
Portanto, no eixo :
E no eixo :
Prontinha galerinha, é isto!
