Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 43

Determine as componentes x e y de F_1 e F_2 .

Passo 1

Opa, vamos resolver este exercício.

Queremos as componentes de F_1 e F_2 nos eixos x e y .

O primeiro a se fazer é sempre desenhar o diagrama de corpo livre:

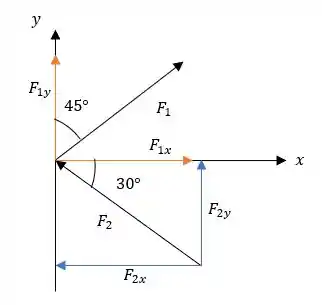
Passo 2

Analisando F_1 , temos que:

sen 45 ° = (F_1 x)/(F_1)

Logo:

F_1 x = F_1 sen 45 °

F_1 x = 200 sen 45 °

F_1 x = 141,42 N

E:

cos 45 ° = (F_1 y)/(F_1)

Logo:

F_1 y = F_1 cos 45 °

F_1 y = 200 cos 45 °

F_1 y = 141,42 N

Passo 3

Analisando F_2 , temos que:

cos 30 ° = (- F_2 x)/(F_2)

Logo:

F_2 x = - F_2 cos 30 °

F_2 x = - 150 cos 30 °

F_2 x = - 129,9 N

O sinal negativo indica a direção negativa com relação ao eixo x .

E:

sin 30 ° = (F_2 y)/(F_2)

Logo:

F_2 y = F_2 sen 30 °

F_2 y = 150 sen (30 °)

F_2 y = 75 N

Resposta

F_1 x = 141,42 N

F_1 y = 141,42 N

F_2 x = - 129,9 N

F_2 y = 75 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um praticante de exercício começa com seu braço na posição relaxada O A , na qual a fita elástica não está esticada. Ele então gira seu braço para a posição horizontal O B . O módulo elástico da fita
Substitua a força de 12k N atuando no ponto A por um sistema força-binário no ( a ) ponto O e ( b ) pontoB .
Calcule o momento combinado de duas forças de 400N em relação ao a ponto O e ( b ) ponto A .
Substitua o sistema força-binário no ponto O por uma única força. Especifique a coordenada y A do ponto sobre o eixo y através do qual passa a linha de ação dessa força resultante
A vista de topo de uma porta giratória é mostrada. Duas pessoas se aproximam simultaneamente da porta e exercem forças de módulo igual, como mostrado. Se o momento resultante em relação ao eixo de rot