29. Determine o momento de cada força em relação ao parafuso localizado em A. Considere , .
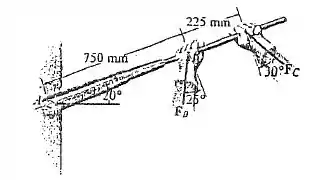
Passo 1
Para resolver esse problema precisamos adotar nossos eixos x e y de forma estratégica a facilitar nosso problema.
Vamos adotar o eixo x na linha que passa pelo parafuso e a chave de aperto e o y perpendicular a x, da seguinte maneira
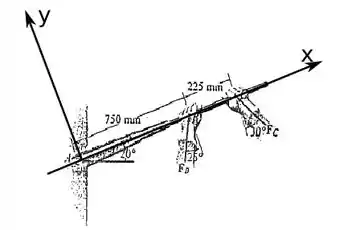
Mas para que isso? Para facilitar nossas contas, já que pelo princípio dos momentos eu posso pegar a componente da força que é perpendicular ao eixo x e calcular o momento a parti dela, a paralela não acrescente nada já que uma força com sua linha de ação passando pelo eixo, não contribui para o momento.
Assim o momento pode ser calculado da seguinte forma:
Onde nesse caso vai ser a componente da força perpendicular a x ( é o ângulo entre a linha de ação da força e uma reta perpendicular à x).
E é a distância do ponto de aplicação da força até o eixo A.
Passo 2
Vamos descobrir as componentes perpendiculares de x das duas forças.
Passo 3
Vamos calcular o momento de cada força.
Resposta
O momento para força B é:
O momento para força C é: