Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 9
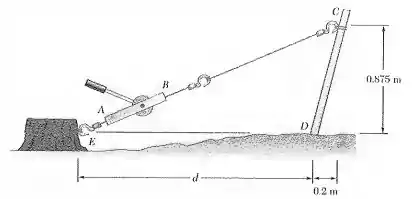
Um guincho AB é usado para endireitar um mourão. Sabendo que a tração no cabo BC é e o comprimento d é 1,9 m, determine o momento em relação a D da força exercida pelo cabo em C decompondo tal força no componente horizontal e no vertical aplicados (a) no ponto C, (b) no ponto E.
Passo 1
Vamos começar entendendo a geometria do problema e calculando alguns ângulos, porque a gente sempre vai precisar dos ângulos pra decompor as forças.
Passo 2
Vamos começar aplicando a força de tração F no ponto C. Como o ângulo do cabo com a horizontal é , temos que as componentes de F são:
O diagrama de corpo livre fica:
Assim, podemos calcular o momento em D. Percebe que as duas componentes vão causar momentos em sentidos contrários, então no somatório de momentos os 2 termos tem sinais diferentes.
Passo 3
Agora vamos pro item b!
Quando aplicamos a força em E, as componentes horizontal e vertical vão ter o mesmo valor absoluto, porque isso só depende da direção da força e a direção do cabo é uma só. Mas os sinais vão mudar porque a tração no cabo vai puxar o ponto D pra direita e pra cima:
O diagrama de corpo livre fica assim:
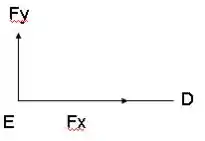
E nesse caso, a componente em x não vai fazer momento, porque o ponto E estão na mesma altura que o ponto D, então cruza a linha do ponto D. O momento vai ficar:
Achamos o mesmo resultado!
Isso faz sentido porque é a mesma situação física. O resultado não deveria mudar pela forma como a gente escolhe fazer a conta.