Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 5
Uma força P de é aplicada em uma alavanca de câmbio. Determine o momento de P sobre B quando é igual a .
Passo 1
Diagrama do corpo livre:
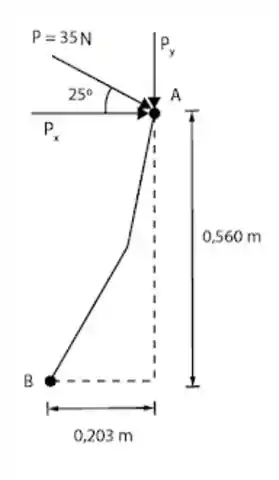
Passo 2
Vamos começar decompondo a força P:
Analisando a componente vertical, podemos perceber que ela produz um momento no sentido horário em B. A componente horizontal também:
O momento é no sentido horário
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A presilha no topo de um mastro suporta as duas forças mostradas. Determine o módulo de T → que não causará momento (momento nulo) no ponto O .
A força de 120N é aplicada em uma extremidade da chave curva, como mostrado. Se α = 30 ° , calcule o momento de F em relação ao centro O do parafuso. Determine o valor de α que maximizaria o momento e
Se o momento combinado das duas forças em relação ao ponto C é zero, determine:(a) o módulo da força P → ;(b) o módulo R da resultante das duas forças;(c) as coordenadas x e y do ponto A sobre a perif
A alavanca de controle está submetida a um momento de 80N ∙ m no sentido horário, exercido pelo seu eixo em A e está projetado para operar com um puxão de 200N , como mostrado. Determine a dimensão x
F4.8. Determine i momento resultante produzido pelas forças em relação ao ponto O.