Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 29

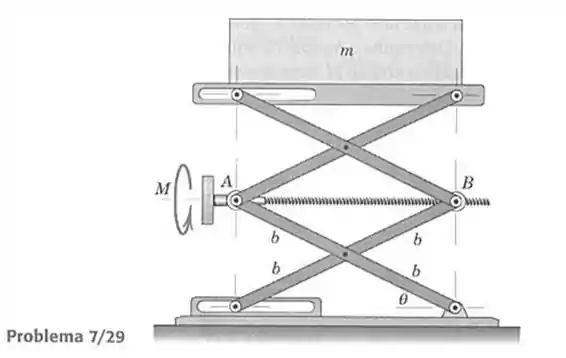
29- A elevação da carga de massa m é controlada pelo parafuso de ajuste que une as juntas A e B . A variação da distância entre A e B para uma revolução do parafuso é igual ao passo L do parafuso (avanço por revolução). Se um momento M f é necessário para vencer o atrito nas roscas e no mancal de escora do parafuso, determine a expressão para o momento total M , aplicado ao parafuso de ajuste, necessário para levantar a carga.

Passo 1

Para entender esse exercício precisamos conseguir ver duas coisas.

Que o parafuso a medida que rotaciona um ângulo d β ele recua uma distância d x (uma parte fica para fora desse triângulo), isso faz o triângulo isósceles A B C ter uma base menor, aumentando o ângulo θ e por consequência subir a posição da carga.

O que faz termos uma relação entre o ângulo de giro e o avanço como:

L 2 π = - δ x δ β

δ β = - 2 π L   δ x

Essa equação nos diz que quanto mais avançamos com o parafuso menor a distância de x .

Passo 2

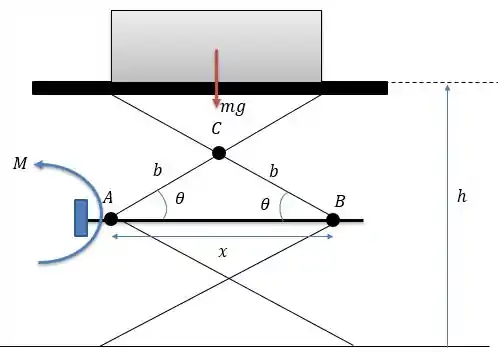
Aplicando a propriedade de trabalhos virtuais conseguimos escrever que:

M δ β - m g δ h = 0

A altura h pode ser expressada pela altura dos quatro triângulos isósceles na estrutura.

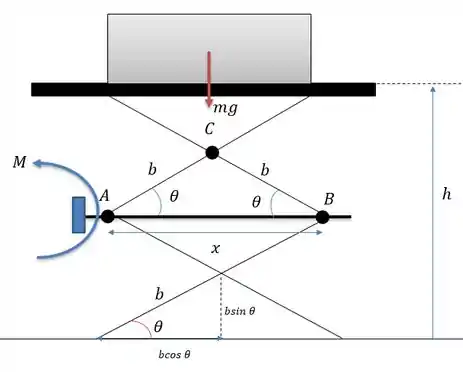
Descobrindo os valores pelo ângulo θ do triângulo retângulo, nós encontramos:

h = 4 b sin ⁡ θ

x = 2 b cos ⁡ θ

Logo:

δ β = - 2 π L   δ ( 2 b cos ⁡ θ ) = 4 b π L sin ⁡ θ δ θ

Logo:

M 4 b π L sin ⁡ θ δ θ - m g δ ( 4 b sin ⁡ θ ) = 0

M 4 b π L sin ⁡ θ δ θ = 4 m g b cos ⁡ θ   δ θ

M = m g L π   c o t g   θ

Porém precisamos adicionar um momento M f de resistência das juntas, logo:

M = M f + m g L π   c o t g   θ

Resposta

M = M f + m g L π   c o t g   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. Deduza uma expressão para a intensidade da força Q necessária para manter o equilíbrio do mecanismo mostrado na figura.
10. Resolva o Problema 10.9 considerando que a força P aplicada no ponto A atua horizontalmente para a esquerda.
3. Determine o binário M que deve ser aplicado ao elemento A B C para se manter o equilíbrio do sistema articulado.
12. A haste fina A B é presa a um colar A e repousa sobre uma pequena roda em C . Desprezando o raio da roda e o efeito do atrito, deduza uma expressão para a intensidade da força Q necessária para se
5. Sabendo que a força de atrito máxima exercida pela garrafa sobre a rolha é 270N , determine ( a ) a força P que se deve aplicar ao saca-rolhas para abrir a garrafa, ( b ) a força máxima exercida pe