Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 178
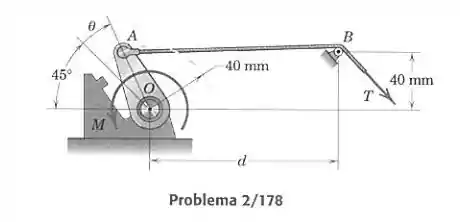
A alavanca de controle gira na faixa . Uma mola de torção interna exerce um momento de retorno na alavanca em torno do ponto dado por onde e está em radianos. Determine e mostre em um gráfico em função de a força trativa necessária para tornar nulo o momento resultante em torno de . Use dois valores para () e comente sobre os méritos relativos do projeto. Os efeitos do raio da polia em são desprezíveis.
Passo 1
Queremos calcular o momento que a força causa no ponto para igualar a . Para isso, precisamos primeiro achar a expressão das coordenadas do ponto em função de e depois calcular:
Passo 2
Seja o eixo orientado pra direita e o eixo para cima, se move num círculo de raio em torno da origem, começando em para e terminando em para . Temos então a equação polar das coordenadas de :
Passo 3
Agora que temos o vetor , podemos obter o vetor , e através dele achar o vetor unitário que define a direção de . Vamos chamar de para simplificar. Temos:
O módulo de é então:
Então achamos o valor do vetor unitário:
Passo 4
Agora já achamos nosso vetor
E calculamos o momento causado pela força:
Resolvendo o produto vetorial, achamos o momento causado pela tração:
Passo 5
Já vimos que o que queremos é que o momento causado pela tração seja cancelado pelo momento de retorno da alavanca. Então:
O valor está positivo pois agora comparamos só os módulos. Isso nos leva ao valor de :
Mostramos aqui o gráfico para e em radianos:
Agora o gráfico para :
