Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 28

30- Expresse a força compressiva C no cilindro hidráulico da plataforma para carros em termos do ângulo θ . A massa da plataforma é desprezível comparada com a massa m do veículo.

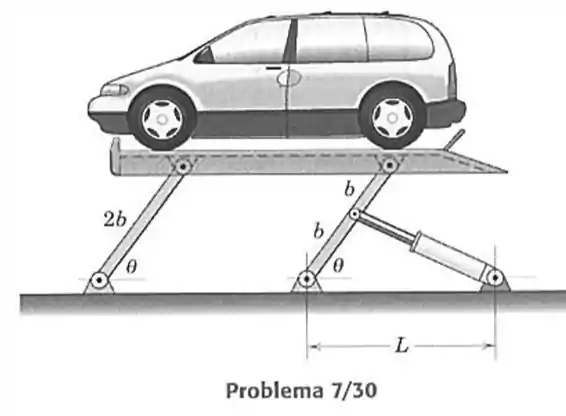
Passo 1

Vamos desenhas os componentes e as forças externas abaixo:

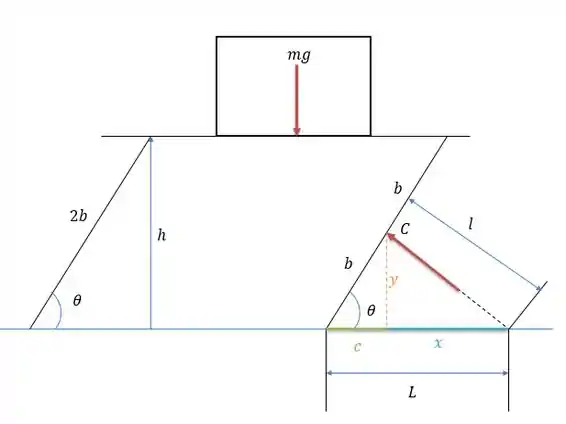
Pela figura acima podemos dizer que a somatória dos trabalhos virtuais que:

δ U = 0

- m g δ h + C δ l = 0

Onde h pode ser achado pelo triângulo esquerdo onde:

sin ⁡ θ = h 2 b → h = 2 b sin ⁡ θ

Logo δ h será:

δ h = 2 b cos ⁡ θ   δ θ

Passo 2

O valor de δ l será encontrado pelo triângulo direito pelos catetos x e y , primeiramente y valerá:

sin ⁡ θ = y b → y = b sin ⁡ θ

Pelo cosseno o valor de c que será:

cos ⁡ θ = c b → c = b c o s   θ

Como L = c + x logo x valerá:

x = L - b c o s   θ

Agora fazendo Pitágoras com os valores de x e y acharemos l :

l 2 = x 2 + y 2

l 2 = L - b c o s   θ 2 + b s i n   θ 2

l 2 = L 2 - 2 b L c o s   θ + b 2 cos 2 ⁡ θ + b 2 sin 2 ⁡ θ

l 2 = L 2 - 2 b L c o s   θ + b 2 ( cos 2 ⁡ θ + sin 2 ⁡ θ )

l 2 = L 2 - 2 b L c o s   θ + b 2

Derivando (sabendo que L   e b são constantes:

2 l   δ l = 2 b L s i n   θ δ θ

δ l = b L l sin ⁡ θ   δ θ

Passo 3

Agora aplicando esses δ na equação do trabalho virtual teremos:

- m g 2 b cos ⁡ θ   δ θ + C b L l sin ⁡ θ   δ θ

Com l = L - b c o s   θ 2 + b s i n   θ 2 , logo C valerá:

C b L sin ⁡ θ L - b c o s   θ 2 + b s i n   θ 2 = 2 m g b cos ⁡ θ

C = 2 m g L   c o t g   θ × L - b c o s   θ 2 + b s i n   θ 2

Resposta

C = 2 m g L   c o t g   θ × L - b c o s   θ 2 + b s i n   θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

28- A balança postal consiste de um setor circular de massa m 0 articulado em O e com centro de massa em G . O prato e a haste vertical A B tem massa m 1 e são articulados ao setor circular em B . A e
32- Uma chave de boca antitorque é projetada para ser usada por um tripulante de uma nave espacial onde ele não tem uma plataforma estável contra a qual se empurrar enquanto aperta um parafuso. O pino
31- Determine a força N exercida na tora por cada garra do pegador de lenha mostrado.
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C . As con
68- A figura mostra a vista lateral de uma claraboia uniforme de massa m e com centro de massa na metade da distância entre A e O . A clarabóia é contrabalançada pela ação da mola, que tem uma rigidez