Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 28

28- A balança postal consiste de um setor circular de massa m 0 articulado em O e com centro de massa em G . O prato e a haste vertical A B tem massa m 1 e são articulados ao setor circular em B . A extremidade A é articulada a haste uniforme A C de massa m 2 , que, por sua vez, é articulada ao suporte fixo. A figura O B A C forma uma paralelogramo e ângulo G O B é um ângulo reto. Determine a relação entre a massa m a ser medida e o ângulo θ , considerando que θ = θ 0 quando m = 0 .

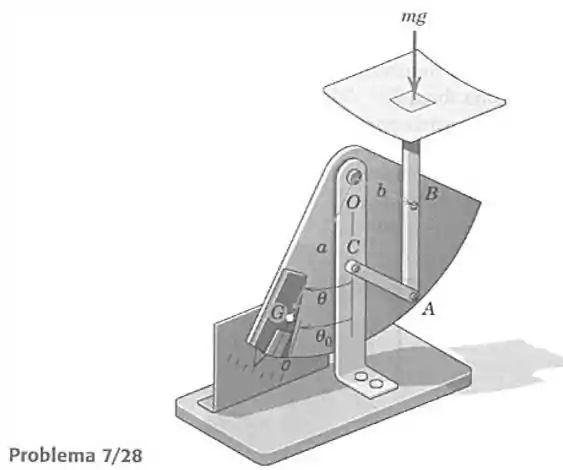
Passo 1

Para resolver esse exercício vamos planificar nossas hastes e elementos principais ,com o objetivo de conseguir ver a influência de movimento das forças na mesma.

Além de rebater o ângulo θ dentro do paralelogramo, e aproveitando que o ângulo de G O B é 90 graus logo o complemento C O B   é de 90 - θ . Com isso só rebater esse ângulo com o ângulo oposto do paralelogramo que por seu um paralelo gramo será igual. E com isso só rebater aplicar a propriedade dos ângulos.

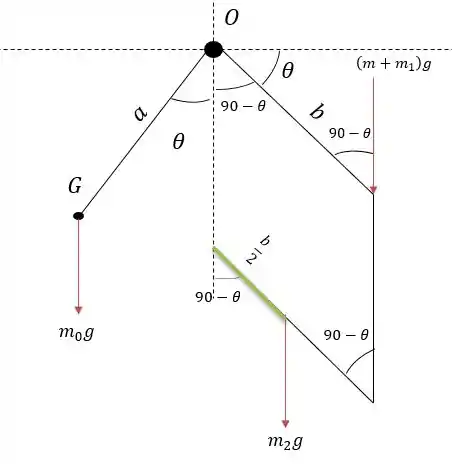
Como a massa da haste C A tem uma massa de m 2 , logo a força peso dessa barra está no meio dessa barra.

Nessas horas que precisamos saber rebater os ângulos e também saber que:

cos ⁡ a - b = cos ⁡ a cos ⁡ b + sin ⁡ a sin ⁡ b

Logo cos ⁡ 90 - θ = sin ⁡ θ .

Passo 2

Agora podemos aplicar a seguinte equação de trabalho virtual.

δ U = 0

Porém para gerar trabalho as forças precisam estar paralelas as barras de ação. Por partes.

A força gerada pelas massas de m e m 1 faz um trabalho na distância O B . Tornando essa barra paralela nós teremos trabalho igual a:

U O B = m + m 1 g [ b sin ⁡ θ ]

O trabalho gerado pela força de massa m 0 na barra de O G será de:

U 0 G = m o g [ acos ⁡ θ ]

Agora pela massa m 2 até o meio da barra C A será:

U C A = m 2 g b 2 cos ⁡ 90 - θ = m 2 g b 2 sin ⁡ θ

Agora fazendo a somatória desses trabalhos, derivando em relação a θ e igualando a zero nós teremos:

m + m 1 g b   δ ( sin ⁡ θ ) + m 0 g a   δ ( cos ⁡ θ ) + m 2 g b 2   δ ( sin ⁡ θ ) = 0

Fazendo a derivada em relação a θ nós teremos:

m + m 1 b g cos ⁡ θ   d θ - m 0 a g s i n   θ   d θ + m 2 b g 2 cos ⁡ θ     d θ = 0

Cortando d θ e g nós teremos:

m + m 1 b cos ⁡ θ + m 2 b 2 cos ⁡ θ = m 0 a sin ⁡ θ

Dividindo os dois lados por cos ⁡ θ   nós teremos:

m + m 1 b + m 2 b 2 = m 0 a   t g   θ

Passo 3

Agora podemos aplicar a condição inicial, que é quando θ = θ 0 → m = 0

Logo:

m 1 + m 2 2 b = m 0 a   t g   θ 0

Agora podemos eliminar as massas m 1 e m 2 ao aplicar essa última equação na que achamos no final do passo 2 . O que nos dá:

m b + m 0 a   t g   θ 0 = m 0 a   t g θ

Isolando m temos:

m b = m 0 a t g   θ - t g   θ 0

m = m 0 a b t g   θ - t g   θ 0

Resposta

m = m 0 a b t g   θ - t g   θ 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

73- Os roletes nas extremidades da barra uniforme A B , de 10k g , se movem livremente nas guias horizontal e vertical, como mostrado. Determine a posição de equilíbrio θ para a barra sob a ação de um
71- O painel retangular uniforme de massa m e centro de massa em G é guiado por roletes- o par superior na guia horizontal e o par inferior na guia vertical. Determine a força P , aplicada a extremida
72- O disco uniforme de alumínio com raio R e massa m rola sem deslizar sobre a superfície circular fixa de raio 2 R . Um cilindro de chumbo também de massa m está preso ao disco e seu centro está loc
76- Determine o ângulo θ para haver equilíbrio da conexão uniforme de 10k g e centro de massa em G , a medida que sua posição no plano vertical é influenciada pela força horizontal de 80N aplicada a s
75- A barra O A , que tem uma massa de 25k g e centro de massa em G , é articulada em torno de sua extremidade O e balança no plano vertical sob a restrição do contrapeso de 10k g . Escreva a expressã