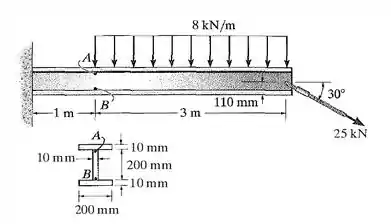
30. A viga de abas largas está sujeita às cargas mostradas. Determine a tensão principal na viga no ponto A e no ponto B. Esses pontos estão localizados na parte superior e na parte inferior da alma, respectivamente. Embora a precisão não seja muito boa, use a fórmula do cisalhamento para calcular a tensão de cisalhamento.
Passo 1
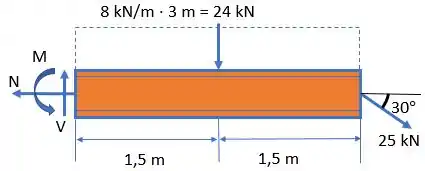
Primeiro, vamos calcular os esforçoes cortantes e os momentos fletores da viga.
Montaremos, então, o diagrama de esforços cortantes e momento fletor no ponto (ou ):
Passo 2
Agora, vamos calcular o centroide da seção transversal. Sabemos que o centroide é dado pela média ponderada das áreas retangulares e seus respectivos centroides no eixo.
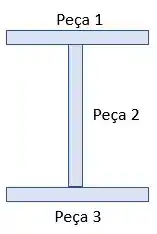
Como as peças são iguais, as áreas serão iguais:
Perceba que o centro de gravidade acontece exatamente na metade da peça.
Passo 3
Devemos, então, calcular o momento de inércia da seção transversal. Sabemos que para seções retangulares, temos a seguinte equação de momento de inércia:
Onde é o tamanho da parede paralela ao eixo e é o tamanho da parede perpendicular ao eixo.
Neste caso, devemos usar o Teorema dos Eixos Paralelos, pois os centroides das peças separadas não estão no mesmo eixo que o centroide da peça total. Esse teorema é dado por:
Onde é a área de um elemento separado e é a distância do seu centroide com o centroide da peça total.
Mas como o centroide da peça 2 coincide com o centroide da peça total, não será preciso aplicar o teorema dos eixos paralelos para ela:
Passo 4
Como nossos cálculos anteriores eram comuns aos dois pontos do enunciado, iremos dividir a questão, resolvendo primeiro que foi pedido para o ponto e depois para o ponto .
Vamos fazer o cálculo da tensão no ponto :
Agora, façamos o cálculo da tensão máxima de cisalhamento no ponto :
Passo 5
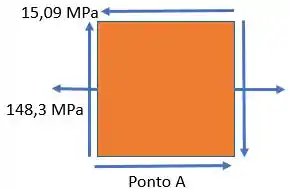
Em seguida, calcularemos, então, as tensões principais no ponto :
Obtemos duas tensões, uma máxima e uma mínima :
Passo 6
Fazendo as contas agora para o ponto , temos que:
Primeiro, obter o cálculo da tensão no ponto :
Segundo, fazer o cálculo da tensão máxima de cisalhamento no ponto :

Passo 7
Terceiro, fazer o cálculo das tensões principais no ponto :
Onde novamente obtemos duas tensões, e
Resposta
As tensões principais no ponto são:
E as tensões no ponto são: