A barra é mantida em equilíbrio por pinos em . Observe que o apoio em tem uma única orelha, o que envolve cisalhamento simples no pino, e o apoio tem orelha dupla, o que envolve cisalhamento duplo. A tensão de cisalhamento admissível para ambos os pinos é . Se uma carga uniformemente distribuída for colocada sobre a barra, determine sua posição admissível mínima em relação a . Cada um dos pinos tem diâmetro de . Despreze qualquer força axial na barra.
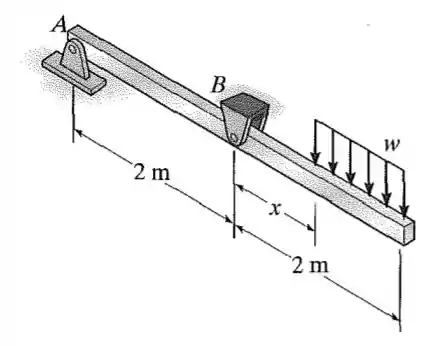
Passo 1
Queremos encontrar a distância mínima em relação a Para isso, vamos calcular os momentos em e em a fim de obtermos equações que dependam só das forças em e só das forças em . Desse jeito, vamos admitir em seguida falha nos pinos e nos pinos encontrando 2 valores de e o valor que nos interessará será o maior entre os 2. Adotando o sentido anti -horário como positivo vamos ter as seguintes equações de momento
Passo 2
Admitindo falha no pino vamos ter
Substituindo esse valor em vamos encontrar . Agora, admitindo falha no pino teremos
Esse valor vamos substituir em obtendo, assim, . Logo, o valor que usaremos será o maior entre esses 2 encontrados, portanto, .