O disco uniforme de gira livremente em relação a um eixo horizontal através de . Uma barra esbelta de é fixada ao disco conforme indicado. Se o sistema é levemente deslocado do repouso enquanto está na posição mostrada, determine a sua velocidade angular após ter girado de .
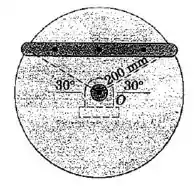
Passo 1
Vamos começar fazendo um esquema do movimento antes e depois da rotação de :
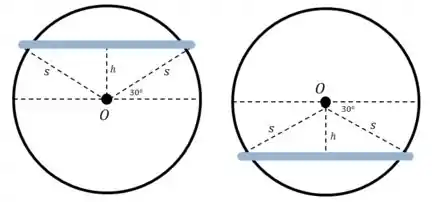
Como o sistema parte do repouso, o que acontece aqui é uma conversão de energia potencial gravitacional em energia cinética de rotação.
Passo 2
Vamos encontrar uma expressão para a variação de energia potencial gravitacional.
O centro de massa do disco permanece parado, mas o centro de massa da barra é deslocado por uma altura , então:
E olhando para o desenho, sabendo que , podemos calcular o valor de :
Ou seja:
Passo 3
E agora precisamos de uma expressão para a energia cinética de rotação do sistema:
Já que a velocidade angular em torno do ponto é a mesma para o sistema inteiro. Vamos calcular esse momento de inércia:
E para o momento de inércia da barra, em relação ao centro do disco, vamos precisar do teorema dos eixos paralelos:
E podemos calcular o comprimento a partir do nosso desenho:
Então:
Agora podemos substituir na nossa expressão para a energia cinética:
Passo 4
Por fim, vamos voltar na nossa lei de conservação da energia:
Resposta
A velocidade angular será .