Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 137
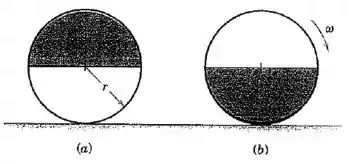
O disco semicircular de massa está montado no aro leve de raio e é liberado a partir do repouso na posição (a). Determine a velocidade angular do aro e a força normal sob o aro quando passa na posição (b) após girar por . O aro rola sem deslizar.
Passo 1
Vamos começar pensando em como a energia se comporta nesse movimento. Para isso vamos dar uma olhada em como a posição do centro de massa muda após um giro de :
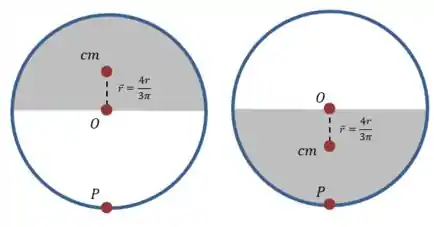
Onde foi consultado em uma tabela:
Entre esses dois instantes, o centro de masssa terá se deslocado pela seguinte altura:
E com isso podemos calcular a variação da energia potencial gravitacional:
E pela lei de conservação de energia:
Passo 2
Então agora precisamos encontrar uma expressão para a variação de energia cinética. Inicialmente, poderíamos pensar em usar essa fórmula:
Onde é a velocidade do centro de massa e é o momento de inércia do corpo em relação a um eixo que passa pelo centro de massa.
Mas se tomarmos o momento de inércia em relação ao ponto onde a roda faz contato com o chão, a expressão fica bem mais simples:
Já que em qualquer instante, uma vez que estamos rolando sem deslizar.
Passo 3
Vamos usar o teorema dos eixos paralelos para calcular (no instante mostrado no nosso segundo desenho):
E usar o mesmo teorema outra vez para calcular , já que o centro de massa não está no centro da roda:
Então:
Já que o aro tem massa desprezível, o momento de inércia incluirá apenas o disco semicircular, e esse valor pode ser consultado em uma tabela:
Agora vamos simplificar essa expressão:
Passo 4
Finalmente, vamos voltar à lei de conservação de energia:
Passo 5
Para calcular a força normal, vamos aplicar a segunda lei de Newton sobre o centro de massa do sistema na direção centrípeta:
Onde é a distância do centro de massa até o ponto em torno do qual ele gira:
Então:
Resposta
A aceleração angular é e a força normal é .