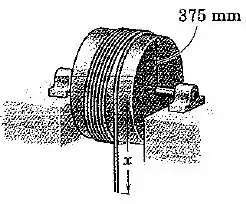
O tambor de de raio e seu eixo possuem uma massa de e um raio de giração de em relação ao eixo de rotação. Um total de de cabo de aço flexível com uma massa de por metro de comprimento está enrolado em volta do tambor com uma extremidade fixada à superfície do tambor. A extremidade livre do cabo tem uma parte inicial pendurada quando o tambor é liberado a partir do repouso. Determine a velocidade angular do tambor para o instante em que . Suponha que o centro de massa da porção do cabo restante no tambor se encontra na linha central do eixo quando . Despreze o atrito

Começamos com as energia cinéticas.

O enunciado já deu a massa e o raio de giração do tambor, que terá apenas energia cinética de rotação, então:

Agora vamos olhar para a parte do cabo que está pendurada, sabendo que essa parte tem um comprimento :

Onde nós reescrevemos a massa como e a velocidade linear do centro de massa do cabo como :

E por último vamos calcular a energia cinética da parte do cabo que está enrolada no tambor. Como o cabo tem um comprimento total de , a parte enrolada tem comprimento :

Então:

Agora vamos encontrar uma expressão para a variaçaõ de energia potencial gravitacional.

Como inicialmente já tínhamos de cabo pendurado, e no final das contas passamos a ter , a massa da porção de cabo que desceu é:

E qual foi o deslocamento do centro de massa dessa porção de ? O centro de massa dessa porção está exatamente no metade do caminho entre as duas extremidades:

Mas o nosso zero da energia potencial está na altura do eixo de rotação, então temos que considerar ainda os de corda que já estavam pendurados:

E então a energia potencial gravitacional é:

E então, voltando à nossa lei de conservação da energia: