Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 128
A alavanca de com de raio de giração em relação a está inicialmente em repouso na posição vertical (), onde a mola anexa de rigidez está sem deformação. Calcule o momento constante aplicado à alavanca através de seu eixo em que dará à alavanca uma velocidade angular quando a alavanca atingir a posição horizontal .
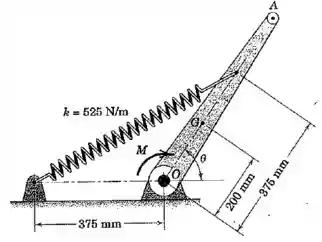
Passo 1
Vamos aplicar a lei de conservação de energia, considerando que o sistema recebe um trabalho aplicado pelo momento :
No estado inicial (em que ), a mola está sem deformação, e a alavanca está em repouso, portanto a única energia que o sistema tem é potencial gravitacional da alavanca:
Onde é a altura do centro de massa em relação à altura do ponto .
Quando tivermos , a energia potencial gravitacional da alavanca será nula, pois estará na altura do ponto . Então teremos apenas as seguintes energias:
Onde é a energia cinética de rotação da alavanca em torno do ponto , e é a energia potencial elástica da mola deformada.
Passo 2
Precisamos determinar as expressões para essas duas energias:
E para a energia potencial elástica da mola:
Agora precisamos determinar a variação do comprimento da mola. O comprimento inicial era:
E o comprimento final é:
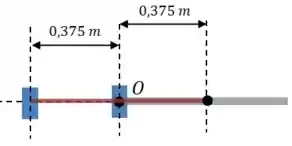
Então:
Passo 3
Agora vamos voltar à nossa equação de conservação de energia:
E como esse trabalho foi realizado por um momento , que provocou um deslocamento angular :
Resposta
O momento aplicado à alavanca deve ser .