Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 4
Na vista lateral de um televisor de apoiado em uma estante de , os centros de massa estão marcados como e . Determine as forças de reação em e . (Note que o centro de massa da maioria dos televisores é localizado bem à frente devido ao peso da parte da frontal dos tubos de imagem.)
Passo 1
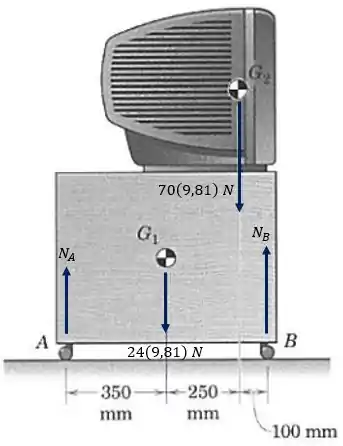
Pessoal, vamos começar desenhando as forças que agem sobre o nosso sistema televisor-estante. Lembre-se de que elas são: peso da estante atuando em , peso do televisor atuando em , reação normal atuando em e reação normal atuando em .
Passo 2
Considerando que o sistema não gira, a resultante dos momentos de cada força em relação ao ponto é nulo. Ou seja:
Passo 3
Além disso, devemos ter resultante de forças nula:
Resposta
Exercícios de Livros Relacionados
A viga uniforme tem massa de 50k g por metro de comprimento. Calcule as reações no apoio O . As cargas mostradas estão em um plano vertical.
Três cabos estão unidos no anel de junção C . Determine as forças trativas nos cabos A C e B C causadas pelo peso do cilindro de 30k g .
Uma força axial de 700N é necessária para remover a polia de seu eixo. Que força F deve ser exercida nos cabos dos dois pés-de-cabra? O atrito nos pontos de contato B e E é suficiente para impedir des
Uma pessoa segura uma mala de 30k g pela alça como indicado na figura. Determine a força trativa em cada uma das quatro argolas idênticas A B .
Para facilitar a mudança de posição de um gancho para levantar carga quando ele está descarregado, usa-se o suporte deslizante mostrado. Os ressaltos em A e B se prendem aos flanges de uma viga caixão