Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 101
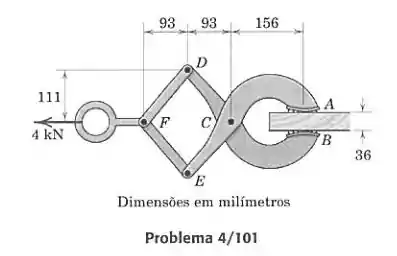
O dispositivo mostrado é usado para arrastar estrados de madeira carregados pelo chão de armazéns. A placa de madeira mostrada é um dos diversos elementos que compõem a base do estrado. Para a carga de 4 kN aplicada por uma empilhadeira, determine o módulo da força suportada pelo pino e as forças normais de aperto em e .
Passo 1
Vamos isolar a parte num diagrama de corpo livre. As forças que atuam nela são a força do elemento , a reação em e a reação em . A força em é obrigatoriamente vertical, pois pela simetria, se um lado fizer uma força para a esquerda(ou direita) o outro lado também deve fazer, e então o pino em nunca estaria em equilíbrio.
Passo 2
Temos 4 incógnitas para esse corpo, então não conseguimos resolver só com as equações dele. Se olharmos para o pino , vemos que os elementos e suportam uma carga de 4 kN para a esquerda:
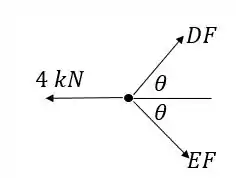
Vamos calcular o ângulo , através de sua tangente:
Pela simetria, as duas forças e são iguais. Então:
Passo 3
Agora que já temos e seu ângulo com a horizontal conseguimos achar diretamente fazendo o momento em torno de :
Substituindo o valor de encontramos :
Passo 4
Como só queremos a força vertical em e essa é a nossa única incógnita nessa direção, fazemos a soma das forças em ser zero:
Substituindo os valores já encontrados:
Pela simetria, temos também do outro lado