Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 41

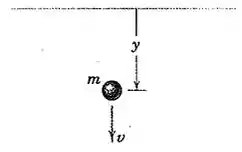
3/41) Em um ensaio de resistência ao movimento em um banho de óleo , uma pequena esfera de aço com massa m é liberada apartir do repouso na superfície ( y = 0 ) . Se a resistência ao movimento é dada por R = k v , onde k é uma constante , desenvolva uma expressão para a profundidade h necessária para a esfera atingir a velocidade v .

Passo 1

Então pessoal , reparem que a esfera está sujeita apenas forças na direção do eixo y . Sendo assim , temos que :

∑ F y = m a y

Representando todas as forças que atuam no corpo , achamos que :

m g - k v = m a

Reparem que a força de resistência é negativa pois se opõe ao movimento . Isolando a , obtemos que :

a = g - k m v

Passo 2

Bom galera , como demonstrado no exemplo 3/5 desta seção , temos que é válida a relação :

v d v = a d y

Sendo assim ,

d y = v d v a

Integrando os dois lados e substituindo o valor de a que encontramos no passo anterior :

∫ 0 h d y = ∫ 0 v v d v g - k m v

h = m 2 k 2 g - k m v - g ln ⁡ g - k m v   0 v

Portanto ,

h = m 2 k 2 g ln ⁡ 1 1 - k v m g - m v k

Resposta

h = m 2 k 2 g ln ⁡ 1 1 - k v m g - m v k

E aí , topa fazer mais exercícios com a gente?

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um foguete tem uma aceleração descrita pelo gráfico. Se ele parte do repouso, construa os gráficos v-t e s-t para o movimento no intervalo de tempo 0
A partícula move-se ao longo de uma linha reta com a velocidade descrita pelo gráfico. Construa o gráfico a - s .
Um trem parte da estação A e no, percurso do primeiro quilômetro, ele move-se com aceleração uniforme. Então, pelos próximos 2 quilômetros, move-se com velocidade escalar uniforme. Por fim, o trem des
O carro de corrida tipo Dragster parte do repouso e move-se ao longo de uma pista reta com uma aceleração – desaceleração descrita pelo gráfico. Construa o gráfico v-s para , e determine a distância p
A aceleração de uma lancha de corrida partindo do repouso é descrita pelo gráfico. Construa o gráfico v - s .