Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 136

2/136) A escada de um carro de bombeiros é projetada para ser prolongada na taxa constante l ' = 6   i n / s e ser elevada na taxaconstante θ = 2   g r a u s / s . Quando a posição θ = 50 ° e l = 15   f t é atingida , determine os módulos da velocidade v e da aceleração a do bombeiro em A .

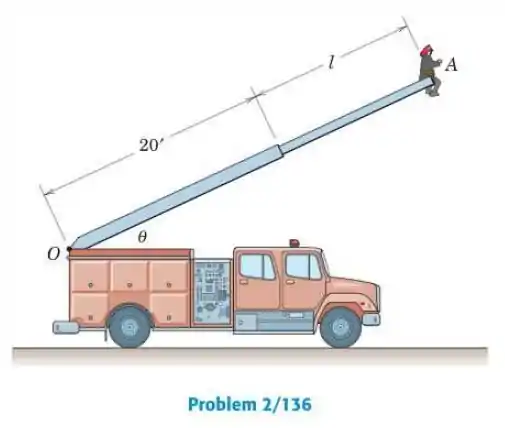
Passo 1

Então galera , de acordo com o enunciado , temos que :

v r = r ' = 6 i n s =   0,5 f t s

Além disso , nós sabemos que :

v θ = r θ '

Para o instante que l= 15 ft, o comprimento total da escada é 35 ft. O fator π/180 aparece para que a taxa 2graus/s seja convertida para rad/seg.

v θ = r θ ' =   35   2 π 180   = 1,222 f t s

Agora tudo fica mais fácil . Basta substituirmos os valores que já conhecemos na fórmula abaixo para calcularmos o valor do módulo velocidade :

v = v r 2 + v θ 2

v = 0,5 2 + 1,222 2 = 1,320   f t / s

Passo 2

Agora para acharmos o módulo da aceleração precisamos primeiramente calcular suas componentes . Temos que :

a r = r " - r θ ' 2

a r = 0 - 35 2 π 180 2

a r = - 0,0426   f t / s 2

Além disso , sabemos que :

a θ = r θ " + 2 r ' θ '

a θ = 0 + 2 ( 0,5 ) ( 2   π 180 ) = 0,0349   f t / s 2

Agora para calcularmos o módulo da aceleração , basta substituirmos na fórmula abaixo os valores encontrados anteriormente :

a = a r 2 + a θ 2

a = 0,0426 2 + 0,03249 2 = 0,0551 f t s 2    

Resposta

v = 1,320   f t / s

a = 0,0551 f t s 2    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os anéis estão conectados por um pino em B e estão livres para se mover ao longo da barra O A e da guia curvilínea O C , tendo o formato de uma cardinoide, r = 0,2 1 + cos ⁡ θ m. Em θ = 30 ° , a veloc
No instante que θ = 45 ° , o atleta está correndo com uma velocidade escalar constante de 2 m/s. Determine a velocidade angular na qual a câmera deve girar a fim de seguir o movimento.
A posição de uma partícula é descrita por r = t 3 + 4 t - 4 m e θ = t 3 / 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 2 s.
Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se sua velocidade angular é θ ˙ = 2 t 2 rad/s, onde t é dado em segundo, determine a intensidade da aceleração da partícula qu
Uma partícula move-se ao longo de uma trajetória circular de raio 5 m. Se sua posição é θ = e 0,5 t rad, onde t é dado em segundos, determine a intensidade da aceleração da partícula quando θ = 90 ° .