Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 141
2/141) O esguicho mostrado gira com uma velocidade angular constante em torno de um eixo horizontal fixo através do ponto . Devido á variação no diâmetro por um fator de , a velocidade da água em relação ao esguicho em A é , enquanto em B é . As velocidade daágua tanto em A quanto em B são constantes . Determine a velocidade e aceleração de uma partícula de água quando esta passa (a) no ponto A e (b) no ponto B .
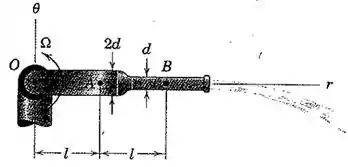
Passo 1
Então pessoal , utilizando as relações que nós conhecemos , obtemos que :
Passo 2
De forma análoga ao passo anterior , calculamos que :
Resposta
Respectivamente , obtemos que ;
Exercícios de Livros Relacionados
O movimento de uma partícula é definido pelas equações x = ( 2 t + t 2 ) m e y = ( t 2 ) m, onde t é dado em segundos. Determine as componentes normal e tangencial da velocidade e aceleração da partíc
As partículas A e B estão se deslocando em torno de uma pista circular a uma velocidade escalar de 8 m/s no instante mostrado. Se a velocidade escalar de B está aumentando na razão de a t B = 4m / s 2
Uma bola é chutada com velocidade escalar inicial v A = 8m / s a um ângulo θ A = 40 ° com a horizontal. Encontre a equação da trajetória, y = f ( x ) , e, em seguida, determine as componentes normal e
Dois ciclistas, A e B, estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 2,4m / s no instante mostrado. Se a velocidade escalar de A é au
As partículas A e B estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 8m / s . Se no instante mostrado a velocidade de A é aumentada na r