Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 18

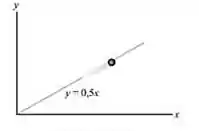
Uma partícula move-se ao longo de uma trajetória de uma linha reta y = 0,5 x . Se a componente da velocidade da partícula é v x = ( 2 t 2 ) m/s, onde t é dado em segundos, determine a intensidade da velocidade e da aceleração da partícula quando t = 4 s.

Passo 1

No problema foi dado a equação que rege o movimento e a componente da velocidade na direção x, então

s ( t ) = ( x ( t ) , y ( t ) )

v ( t ) = ( v x ( t ) , v y ( t ) ) = ( 2 t 2 , v y ( t ) )

Integrando dos dois lados da equação, teremos

d x = v x d t

∫ 0 x d x = ∫ 0 t v x d t

x = 2 t 3 3

Substituindo x ( t ) em y ( x ) iremos obter,

y ( x ) = 0,5 x → y ( t ) = 0,5 ( 2 t 3 3 ) = t 3 3

Sabe-se que

d y d t = v y

Então derivando teremos,

v y = t 2

v ( t ) = ( 2 t 2 , t 2 )

Em t = 4 s,

v ( 4 ) = ( 2 ( 4 ) 2 , 4 2 ) = ( 32,16 )

Com isso, podemos encontrar a resultante da velocidade

v = v x 2 + v y 2 = 3 2 2 + 1 6 2 = 35,78 m/s

Passo 2

Para o cálculo da aceleração da partícula, basta derivar

a ( t ) = d v ( t ) d t = ( 4 t , 2 t ) → a ( 4 ) = ( 16,8 )

Calculando a resultante, teremos

a = a x 2 + a y 2 = 1 6 2 + 8 2 = 17,89 m/s2

Resposta

A velocidade e a aceleração serão, respectivamente v = 35,78 m/s e a = 17,89 m/s2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo caindo com velocidade v 0 colide e mantém contato com a plataforma apoiada por um jogo de molas. A aceleração do corpo após o impacto é a = g - c y , onde c é uma constante positiva e y é medi
O movimento horizontal do êmbolo e do eixo é dificultado pela resistência ao movimento do disco através do banho de óleo. Se a velocidade do êmbolo é v 0 na posição A onde x = 0 e t = 0 , e se a desac
Um corpo que se move em uma linha reta entre dois pontos A e B afastados de uma distância de 50m tem uma velocidade cujo quadrado aumenta linearmente com a distância percorrida, como mostra o gráfico.
Um determinado lago é proposto como uma área de aterrissagem para grandes aviões a jato. A velocidade de aterrissagem de 160k m / h no contato com a água deve ser reduzida para 30k m / h em uma distân
Calcule a velocidade de impacto de um corpo liberado a partir do repouso a uma altitude h = 800k m . (a) suponha uma aceleração gravitacional constante g 0 = 9,81m / s ² ² e (b) considere a variação d