Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 69
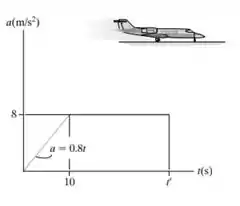
Um avião move-se ao longo de umna pista reta com uma aceleração descrita pelo gráfico. Se ele parte do repouso e precisa de uma velocidade de 90m/s para decolar, determine o comprimento de pista minimo necessário e o tempo t’ para a decolagem. Construa os gráficos v-t e s-t.
Passo 1
Partindo do intervalo de tempo de (0:10) s, podemos resolver a equação diferencial (1) para a obtenção da equação da velocidade no mesmo intervalo.
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 1)
Para t = 10s
Para o interval de
Resolvendo a integrais em ambos os lados, teremos:
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT (2)
Passo 2
Utilizando a Eq.(2), podemos calcular o tempo em na velocidade de 90 m/s
Passo 3
Utilizando a Eq.(3), podemos calcular a equação do espaço em cada intervalo de tempo, então:
Para
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT (3)
s
Para s
m
A partir do mesmo método podemos calcular a equação do espaço para o intervalo (10:t’), então:
Para
Resolvendo as integrais, iremos obter:
Para s, o valor de será:
m
Resposta
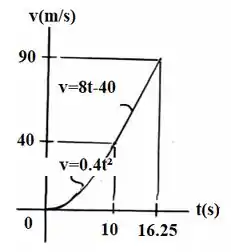
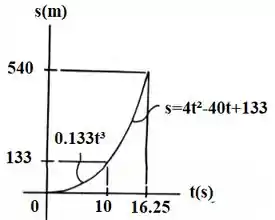
Os gráficos e estão dispostos a seguir:
