Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 92
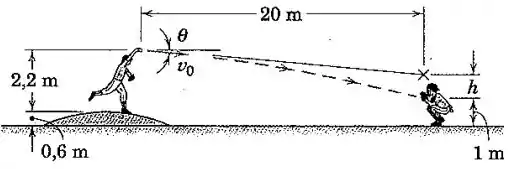
Determine a localização do ponto em direção ao qual o arremessador deve lançar a bola de modo que ela atinja a mão do receptor. A bola é lançada com uma velocidade de .
Passo 1
Galera, pra gente descobrir essa localização , primeiro temos que determinar em qual ângulo o arremessador joga a bola. Como temos todas as dimensões e da mão do receptor, será útil construirmos a equação da trajetória de um projétil desse tipo.
Começamos pela seguinte equação do movimento horizontal:
Agora, a gente escreve a seguinte equação do movimento vertical:
Só resta substituir a expressão de já encontrada:
Então essa é a equação da trajetória da bola lançada da posição com velocidade e fazendo um ângulo com a horizontal, beleza?
Passo 2
Nessa equação, podemos colocar , , e . Também já vamos substituir e , que são as coordenadas da mão do receptor, onde a bola acerta:
Lembrando que , temos:
Aqui temos uma equação quadrática para resolver, e só consideraremos a raiz positiva:
Passo 3
Agora, considere o triângulo retângulo formado a partir do ângulo , o cateto horizontal de e o cateto vertical de medida , onde é a altura inicial de lançamento e é a altura da mão do receptor. Então temos a seguinte relação:
Mas no passo anterior descobrimos que . Logo, teremos: